本节介绍了Eulerian数的两种推广形式：细化Eulerian数和下降多项式.
细化Eulerian数，记作Ad，k，j，为对称群Sd中有k个降序并且最后一个元素为j的排列总数.即
依照上述组合定义可知，Ad，k，j作为Ad，k的细化形式，可以看作是相邻两Eulerian数Ad，k与Ad，k+1之间的一个插值，从而有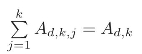
等一系列显然的结论.自然地，人们关心细化Eulerian数是否继承了Eulerian数的一些性质，例如对数凹性和渐近性质.(www.xing528.com)
Ehrenborg，Readdy和Steingr´ımsson[46]将Ad，k，j表示成单位立方体相邻切片Tk与Tk+1的混合体积，从而得到了Ad，k，j关于j的对数凹性.由于Eulerian数Ad，k关于d的渐近形式为Gauss型.人们猜测Ad，k，j也“遗传”了同样的性质.然而在文献[47]中，Mark Conger利用数值实验观察到Ad，k，j随着d值的增大，其渐近形式并非正态分布的现象，但他无法解释这种现象.在此，我们给出细化Eulerian数的样条解释.利用这一解释，得到了细化Eulerian数的显式与递归表达式.同时，也给出了由Hermite正交多项式表示的细化Eulerian数的渐近形式.这就解释了Mark Conger在文献[47]中利用数值实验得到的现象.
细化Eulerian数和许多重要的数学问题相关联.近年来，对细化Eulerian数的研究显得日趋重要.Brenti和Welker[48]将其用于表示单纯复形的重心细分.此后，在Brenti和Welker[48]等人工作的基础上，Martina Kubitzke和Eran Nevo[49]利用代数方法导出了细化Eulerian数的许多新的组合不等式.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
