B样条方法起源于Curry和Schoenberg关于一元样条的研究工作，是定义B样条的几何方法.这种方法的本质是研究高维空间的多面体在较低维空间投影的测度函数.一元B样条是由Curry和Schoenberg 1966年引入的.1976年de Boor将其推广到多元样条.但这种几何定义的推广不便于理论研究，直到便于理论研究的泛函形式出现后，多元B样条的研究才开始活跃起来.多元B样条的泛函形式的推广有多种形式，如单纯形样条、Box样条、锥样条等.分别由Micchelli，de Boor，Dahmen等人给出.Micchelli，de Boor，De Vore，Dahmen等在这方面做了大量的研究工作.与上面的方法相比，B样条方法对剖分的要求更为严格，通常为均匀的剖分.但B样条方法在理论上较为完善，且与许多不同的数学学科都有着深刻的内在联系.下面我们做一简单介绍.
令V={vi，1≤i≤n}⊂Rs，其中vi可重复，使得spanV=Rs.多元B样条Mw（x|V）定义为
其中dt=dt1···dtn，Q为Rn的凸区域.
若取w（t）=n！，Q=Sn，其中Sn为n维单纯形.则由此定义的B样条就是Micchelli引入的单纯形样条，记为M（x|V）.若取w（t）=1，Q=[0，1）n且
，则由此定义的B样条就是de Boor，De Vore引入的Box样条，记为B（x|V）.若取
且
，则由此定义的B样条就是Dahmen引入的锥样条，又称为多元截断幂，记为T（x|V）.
Dirichlet概率密度函数定义为
其中，α0＞0，···，αn＞0.若取w（t）=D（V），Q=[0，1）n，则由此定义的B样条被称为Dirichlet样条MD（t|x0，···，xn），t∈Rs.
下面以Box样条为例，介绍多元B样条的基本性质.
定理1.8 Box样条B（x|V）具有如下性质：(www.xing528.com)
（1）SuppB(x|V)=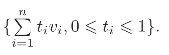
（2）B（x|V）的函数值非负，且在支集内部严格大于0.
（3）B（x|V）是次数不大于n-s的分片多项式.
（4）令μ=min{n（V）|span（S-V）／=Rs}-2，则B（x|V）μ阶光滑.
（5）.B(x|V)*B(x|W)=B(x|V∪W).
我们将在后面的章节里对多元Box样条及多元截断幂进行较为详细的介绍.关于多元B样条更为详细的介绍，可参见文献[21].
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
