低级晶族矿物的光率体

（一）二轴晶光率体的形态

二轴晶光率体的形态是三轴椭球体。二轴晶包括低级晶族的斜方晶系、单斜晶系和三斜晶系的矿物晶体。这三个晶系的晶体对称程度较低，三个结晶轴a、b、c（简称a、b、c轴）方向的轴单位都不相等，表明晶体在三维空间不同方向的内部结构和光学性质是不均一的。

实验可以证明，低级晶族矿物晶体中都有三个互相垂直的方向，光波沿这三个方向振动其相应的折射率是晶体的三个主折射率，分别以符号Ng、Nm、Np表示，它们分别代表矿物的最大、中等、最小折射率，即Ng＞Nm＞Np。二轴晶光率体就是以Ng、Nm、Np为半径的三轴不等的椭球体。下面以黄玉为例说明二轴晶光率体的构成。

黄玉属斜方晶系，三个结晶轴互相垂直，即a⊥b⊥c，a、b、c三个方向的轴单位不相等。

（1）取黄玉垂直b轴切面（即平行a、c轴切面），使光波垂直该切面（即沿b轴方向）入射，发生双折射而分解形成两种偏光。一种偏光振动方向平行a轴，相应的折射率最小，即Np=1.619；另一种偏光振动方向平行c轴，相应的折射率最大，即Ng=1.628。分别以a、c轴为半径方向，以Np、Ng为半径长度，可作出一个垂直光波入射方向的椭圆切面（图1-16A）。

（2）取黄玉垂直c轴切面（即平行a、b轴切面），使光波垂直该切面（即沿c轴方向）入射，发生双折射而分解形成两种偏光。一种偏光振动方向平行a轴，相应的折射率仍为Np=1.619；另一种偏光振动方向平行b轴，相应的折射率为一中间值，即Nm=1.622。同样可作出一个垂直光波入射方向的椭圆切面，其长短半径分别为Nm、Np（图1-16B）。

（3）取黄玉垂直a轴切面（即平行b、c轴切面），使光波垂直该切面（即沿a轴方向）入射，发生双折射而分解形成两种偏光。一种振动方向平行c轴，相应的折射率仍为Ng=1.628；另一种振动方向平行b轴，相应的折射率仍为Nm=1.622。也同样以Ng和Nm为长、短半径可作出一个垂直光波入射方向的椭圆切面（图1-16C）。

将这三个互相垂直的椭圆按照它们彼此的空间关系组合起来，即得到黄玉的光率体（图1-16D）。显然，这是一个以Ng、Nm、Np为主轴的三轴不等的椭球体，即三轴椭球体。

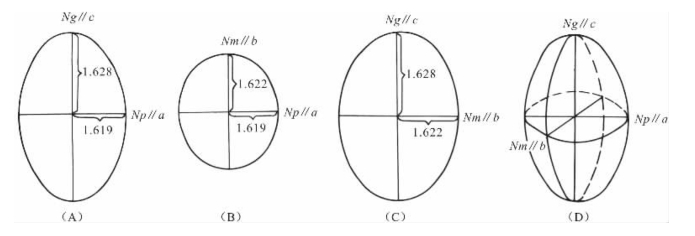
图1-16　二轴晶（黄玉）光率体的构成

（据陈芸菁，1987，修改）

所有二轴晶矿物的光率体，都像黄玉的光率体一样，为三轴椭球体，光率体三个半径（主轴）的长度分别代表矿物三个主折射率Ng、Nm、Np的大小，这是普遍特征。不同种属矿物的光率体的差异在于：三个半径的长短不同；三个半径的方向在晶体中的方位（即光性方位，后述）不同。例如橄榄石属斜方晶系，其光率体的三个半径分别是Ng=1.715，Nm=1.680，Np=1.651；三个半径在晶体中相应的方位是Ng∥a，Nm∥c、Np∥b（也可以写作Ng=a，Nm=c，Np=b）。

（二）二轴晶光率体的要素

三轴椭球体的对称程度比旋转椭球体低，因此二轴晶光率体的要素比一轴晶光率体更为复杂多样。

1.三个主轴

二轴晶光率体中三个互相垂直的轴，称为光率体主轴或光率体对称轴，简称主轴（Princial axis），代表三个主要光学方向。三个主轴分别以Ng、Nm、Np命名，其长度分别代表三个主折射率（Principal refractive index），其相对大小为Ng＞Nm＞Np，其空间方位关系为Ng⊥Nm⊥Np（图1-17A）。

2.三个主轴面

二轴晶光率体中包含两个主轴的面称为主轴面或主截面。显然，共有三个主轴面，即NgNp面、NgNm面、NmNp面。这三个主轴面彼此互相垂直，每一主轴面都垂直于不包含在该主轴面内的另一个主轴（图1-17A）。

不难看出，三个主轴是光率体的二次对称轴，三个主轴面是光率体的对称面，还有一个对称中心，二轴晶光率体的对称型式为3L23PC。

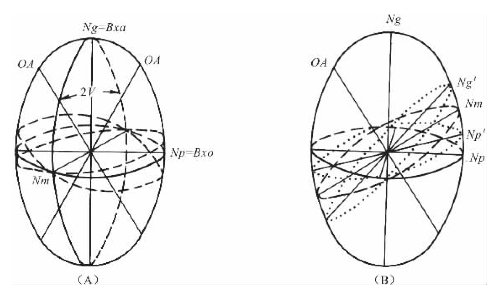
图1-17　二轴晶光率体及其要素

（据陈芸菁，1987，略有修改）
Ng=Bxa、Np=Bxo表示Ng与Bxa重合、Np与Bxo重合^[1]

3.两个圆切面

二轴晶光率体是三轴不等的椭球体，包括中间主轴Nm可以切出一系列与NgNp主轴面垂直的椭圆切面；在NgNp主轴面上，沿椭圆弧从Ng向Np移动，其间必可找到一点，此点至中心的长度恰等于Nm，过此点垂直于NgNp主轴面的切面必为圆切面（Circular section）（图1-17B）。由于三轴椭球体左右对称，NgNm主轴面是对称面，因此这样的圆切面必有两个，对称地分布于NgNm主轴面的左右两侧，并相交于主轴Nm上（图1-17A）。

4.两个光轴

光波沿着垂直于上述两个圆切面的方向入射不发生双折射，也不改变入射光波的振动特点和振动方向，所以这两个圆切面的法线方向就是二轴晶光率体的两个光轴，以符号“OA”表示（图1-17A），二轴晶即由此得名。

5.一个光轴面

包括两个光轴的平面称为光轴面（Optic axial plane），以符号“OAP”表示（有的文献中以Ap表示）。因为圆切面垂直于NgNp主轴面，所以二光轴必位于NgNp主轴面内，即光轴面与NgNp主轴面一致（图1-17A）。垂直光轴面的方向就是主轴Nm，故称Nm主轴为光轴面法线或光学法线。

6.光轴角

绝大多数二轴晶两个光轴相交成一个锐角和一个钝角。两光轴相交的锐角称为光轴角（Optic axial angle），以符号“2V”表示（图1-17A），2V值小于90°。

7.锐角等分线

两光轴所夹锐角的平分线称为锐角等分线（Acute bisectrix），以符号“Bxa”表示。显然，锐角等分线必与主轴Ng（图1-17A）或Np一致。

8.钝角等分线

两光轴所夹钝角的平分线称为钝角等分线（Obtuse bisectrix），以符号“Bxo”表示。钝角等分线必与主轴Np（图1-17A）或Ng一致。

这里需要说明的是，广义地理解，两光轴相交的锐角和钝角都可称为光轴角，因此在光性矿物学和费德洛夫法教材以及其他一些文献中，也常用2VNg或2VNp这样的符号表示光轴角，2VNg、2VNp分别表示以Ng、Np为等分线的光轴角，对于某种具体矿物来说，其数值可以小于90°，也可以大于90°。

上述二轴晶光率体的八个要素可以在光轴面（NgNp主轴面）上直观地标示出来。图1-18表示二轴正晶的光轴面，读者可以自绘一个二轴负晶的光轴面，并把八个光率体要素标出来。

（三）光轴角公式

光轴角的大小可以用晶体光学鉴定方法在偏光显微镜下实测，也可以用主折射率Ng、Nm、Np值计算。

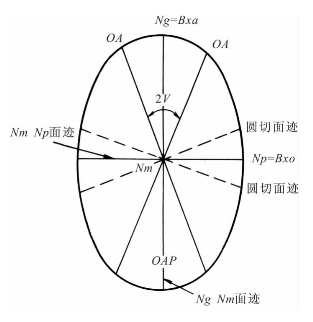
图1-18　二轴正晶光轴面上标出的光率体要素

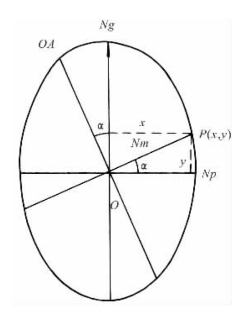
图1-19　光轴角与主折射率关系图

如图1-19所示，设OA与Ng的夹角为α，则圆切面迹线与Np的夹角亦为α。圆切面迹线与椭圆曲线的交点P的坐标为x和y，根据椭圆方程有：

(www.xing528.com)

由于x=Nmcosα，y=Nmsinα，将其代入式（1-3）得：

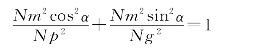
又因为sin2α+cos2α=1，所以上式可写作

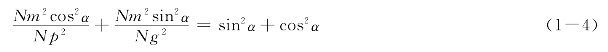
将式（1-4）两边各除以cos2α可得：

整理式（1-5）可得：

式（1-6）即为光轴角公式（Optic angle equation）。此式分子中的Ng2大于分母中的Np2，但分子中的（Nm+Np）小于分母中的（Ng+Nm），可以近似地认为Ng2（Nm+Np）／Np2（Ng+Nm）=1，这样式（1-6）可以简化为：

式（1-7）即为简化的光轴角公式。

（四）二轴晶光率体光性符号的划分和判别

二轴晶光率体虽然都是三轴椭球体，但由于三主轴的长短不同，其形态亦可分为两类：一类是两光轴所夹锐角等分线为Ng轴，钝角等分线为Np轴，Nm轴的长度比较接近Np轴，光率体为相对比较长形的三轴椭球体（沿Ng轴方向伸长）；另一类是两光轴所夹锐角等分线为Np轴，钝角等分线为Ng轴，Nm轴的长度比较接近Ng轴，光率体为相对比较扁形的三轴椭球体（沿Np轴方向压扁）。前一类称为二轴晶正光性光率体，后一类称为二轴晶负光性光率体。若两光轴所夹的角恰好等于90°，则光率体的光性符号不分正负，也可称为中性光率体。具有正光性光率体的晶体（矿物）称为二轴正光性晶体（矿物），简称为二轴正晶，可记作二轴（+）；具有负光性光率体的晶体（矿物）称为二轴负光性晶体（矿物），简称为二轴负晶，可记作二轴（-）。此处的“正”“负”或“+”“-”表示光率体的光性符号，也称矿物的光性符号。

像一轴晶一样，二轴晶的光性符号也是鉴别矿物的重要参数。要判别矿物的光性符号，就必须确定Bxa方向是Ng轴还是Np轴：若Bxa=Ng（Bxo=Np），则光性符号为正；若Bxa=Np（Bxo=Ng），则光性符号为负。在偏光显微镜下，可以应用晶体光学的某些原理和方法确定Bxa方向是Ng轴或Np轴而判断矿物的光性符号正负（详见本书第五章）。

如果用油浸法或其他方法已测定矿物的三个主折射率Ng、Nm、Np，也可以用光轴角公式（非简化式）判别矿物的光性符号。判别方法是，先用前述的光轴角公式（1-6）计算出α值，然后根据α值大小确定矿物的光性符号：

若α＜45°，矿物光性符号为正，光轴角2V=2α；

若α＞45°，矿物光性符号为负，光轴角2V=2（90°-α）。

这里需要说明的是，在本教材以前的一些晶体光学教材和有关文献中，都是根据Ng-Nm与Nm-Np的相对大小确定二轴晶的光性符号的，表述为Ng-Nm＞Nm-Np为正光性符号，Ng-Nm＜Nm-Np为负光性符号。这种表述和判别只有当2V与90°相差较大时才是可行的，即Ng-Nm＞Nm-Np，Nm比较接近Np，圆切面向NmNp主轴面靠近，两个光轴方向均向Ng主轴靠近，故Bxa=Ng，应为正光性符号（图1-20A）；相反，Ng-Nm＜Nm-Np，Nm比较接近Ng，圆切面向NgNm主轴面靠近，两个光轴方向均向Np主轴靠近，故Bxa=Np，应为负光性符号（图1-20B）。但从严格定量意义上说，这种表述和判别是不准确的，有时甚至是错误的。因为这种判别的依据是计算光轴角的简化式，而简化式是由光轴角计算公式的全式省略了Ng2（Nm+Np）／Np2（Ng+Nm）项，数学上可以证明Ng2（Nm+Np）／Np2（Ng+Nm）是恒大于1的，因此简化式与全式是不等效的。例如，当Nm-Np=Ng-Nm时，按简化式计算，tanα=1，矿物光性符号不分正负；但用全式计算，tanα＞1，矿物光性符号为负，因此按简化式判别结果是不准确的，Ng-Nm与Nm-Np的相对大小不能作为判别光性符号的原则。

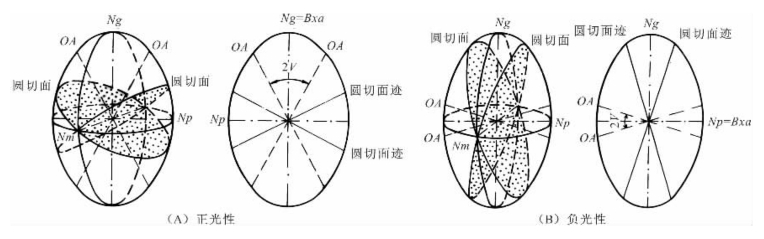
图1-20　二轴晶光率体光性符号的划分

（据季寿元，1961，略有修改）

（五）二轴晶光率体的切面类型

1.垂直光轴（OA）的切面

形态为圆，其半径是Nm。光波垂直圆切面（即沿光轴）方向入射不发生双折射，也不改变入射光波的振动特点和振动方向。光波在圆切面内任何方向振动其折射率都是Nm，故圆切面的双折射率为零。二轴晶有两根光轴，所以圆切面有两个（图1-21A）。

2.平行光轴面（OAP）的切面

形态为椭圆，即NgNp主轴面，其长半径为Ng，短半径为Np。光波垂直光轴面（即沿主轴Nm）方向入射，发生双折射而分解形成两种偏光：一种偏光振动方向平行长半径Ng，其折射率即Ng；另一种偏光的振动方向平行短半径Np，其折射率即Np。该切面双折射率为Ng-Np，是二轴晶矿物的最大双折射率（图1-21B）。

3.垂直锐角等分线（Bxa）的切面

形态为椭圆，按照光符正负不同有两种情况。

二轴正晶，Ng=Bxa，垂直Bxa切面就是主轴面NmNp，切面的光率体椭圆半径分别是Nm和Np。光波垂直该切面（即沿Ng）方向入射，发生双折射而分解形成两种偏光，其振动方向分别平行椭圆的长半径（主轴Nm）和短半径（主轴Np），相应的折射率即为Nm和Np值，该切面的双折射率为Nm-Np（图1-21C）。

二轴负晶，Np=Bxa，垂直Bxa切面就是主轴面NgNm，切面的光率体椭圆半径分别是Ng和Nm。光波垂直该切面（即沿Np）方向入射，发生双折射而分解形成两种偏光，其振动方向分别平行椭圆的长半径（主轴Ng）和短半径（主轴Nm），相应的折射率即Ng和Nm值，该切面的双折射率为Ng-Nm（图1-21D）。

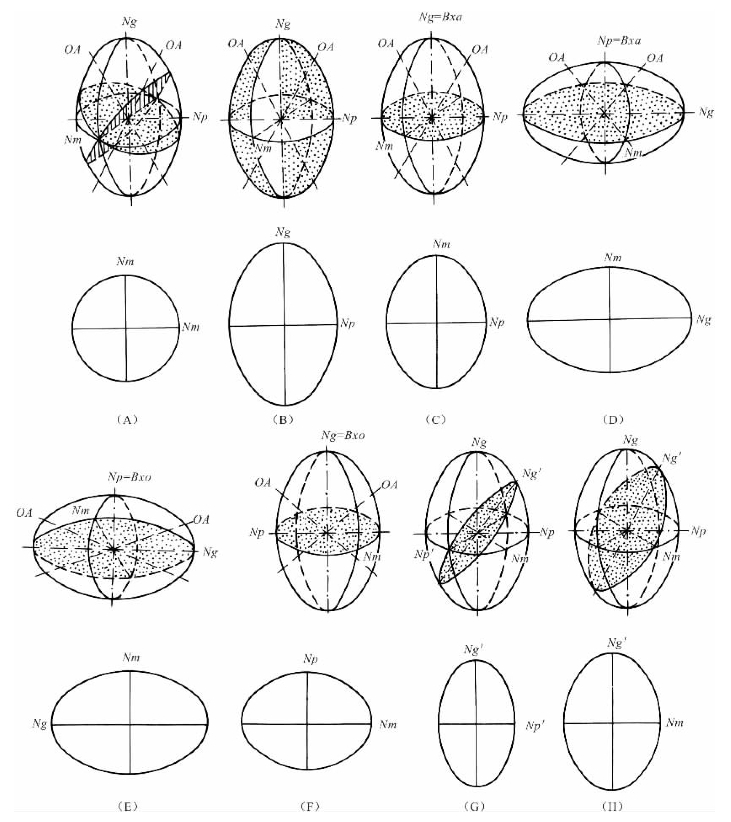
图1-21　二轴晶光率体的切面类型

（据李德惠，1993，修改）
（A）垂直OA切面；（B）平行OAP切面；（C）垂直Bxa切面（+）；（D）垂直Bxa切面（-）；
（E）垂直Bxo切面（+）；（F）垂直Bxo切面（-）；（G）任意斜交切面；（H）垂直OAP的斜交切面

4.垂直钝角等分线（Bxo）的切面

形态为椭圆，按照光符正负不同也有两种情况。

二轴正晶，Np=Bxo，垂直Bxo切面的光率体椭圆长、短半径分别是Ng和Nm（图1-21E）；二轴负晶，Ng=Bxo，垂直Bxo切面的光率体椭圆长、短半径分别是Nm和Np（图1-21F）。光波沿垂直这种切面（即沿Bxo）方向传播，发生双折射而分解形成两种偏光，其振动方向分别平行椭圆的长、短半径，即主轴Ng和Nm（二轴正晶）或主轴Nm和Np（二轴负晶），它们的双折射率分别是Ng-Nm（二轴正晶）、Nm-Np（二轴负晶）。

要特别注意一点，二轴晶矿物无论是正光符或是负光符，一般情况下，垂直Bxo切面的双折射率总是大于垂直Bxa切面的双折射率。因为二轴正晶一般情况下是Ng-Nm（垂直Bxo切面双折射率）＞Nm-Np（垂直Bxa切面双折射率），二轴负晶一般情况下是Ng-Nm（垂直Bxa切面双折射率）＜Nm-Np（垂直Bxo切面双折射率）。

以上四种类型的切面，按双折射率的变化趋势是从平行OAP切面（双折射率最大）→垂直Bxo切面（双折射率较大）→垂直Bxa切面（双折射率较小）→垂直OA切面（双折射率为零）双折射率逐渐减小。

上述四种类型的切面，都是二轴晶光率体中特殊方向的切面，其中平行OAP、垂直Bxa、垂直Bxo三种类型的切面既是主轴面，同时又是垂直光率体另一个主轴的切面。在实际观察矿物晶体薄片时，这些特殊方向的定向切面出现的概率是很小的，更为常见的是除这些特殊方向切面以外的一般斜切面。

5.斜切面

既不垂直光轴也不垂直光率体主轴的切面都是斜切面，又称任意切面。这种切面形态都是椭圆，椭圆的长、短半径分别以Ng′、Np′表示，Ng′变化于Ng和Nm之间，Np′变化于Nm和Np之间，即Ng＞Ng′＞Nm＞Np′＞Np。光波垂直这种斜切面（即沿光轴和主轴之外的任意方向）入射，发生双折射而分解形成两种偏光，其振动方向分别平行于椭圆的长、短半径方向，相应的折射率为Ng′和Np′值。该种切面的双折射率为Ng′-Np′，其数值大小随切面方向的不同变化于零与最大双折射率之间（图1-21G）。

在斜切面中有一种垂直主轴面（或者平行一个主轴）的斜交切面，称半任意切面，包括垂直NgNp主轴面（平行Nm）的斜交切面、垂直NgNm主轴面（平行Np）的斜交切面、垂直NmNp主轴面（平行Ng）的斜交切面三种类型。这类半任意切面形态为椭圆，椭圆的长、短半径中总有一个半径是主轴（Ng或Nm或Np），另一个半径是Ng′或Np′。在这三类半任意切面中，比较重要的是垂直光轴面NgNp（即平行Nm）的斜交切面（图1-21H），因为这种斜切面的椭圆半径中必有一个是主轴Nm，另一个是Ng′或Np′。由于这种切面是包含Nm主轴的切面，理论上讲可以有无穷多个，因此这种切面出现的概率比垂直光轴的圆切面大得多，所以在实际应用中这种切面可以代替垂直光轴的切面，垂直光轴的圆切面实际上就是这种切面之一。