信息表示方法与十进制转二进制计算法

计算机中最基本的工作是进行大量的数值运算和数据处理。在日常生活中，我们较多地使用十进制数，而计算机是由电子元器件组成的，因此，计算机中的信息都得用电子元器件的状态来表示。而与这些状态相对应的数制，就是二进制，同时计算机内只能接受二进制。

计算机为什么要用二进制呢？首先，二进制只需0和1两个数字表示。物理上一个具有两种不同稳定状态且能相互转换的元器件是很容易找到的，如电位的高低、晶体管的导通和截止、磁化的正方向和反方向、脉冲的有或无、开关的闭合和断开等，都恰恰可以与0和1对应。而且这些物理元器件的状态稳定可靠，因而其抗干扰能力强。相比之下，计算机内如果采用十进制，则至少要求元器件有10种稳定的状态，在目前这几乎是不可能的事。其次，二进制运算规则简单，加法、乘法规则各4个，即

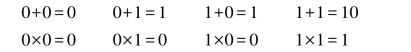
采用门电路，很容易就可实现上述的运算。再次，逻辑判断中的“真”和“假”，也恰好与二进制的0和1相对应。所以，计算机从其易得性、可靠性、可行性及逻辑性等各方面考虑，选择了二进制数字系统。采用二进制，可以把计算机内的所有信息都用两种不同的状态值通过组合来表示。

（1）数制

按进位的原则进行计数，称为进位计数制，简称数制。常用的数制有十进制、二进制、八进制和十六进制。无论哪一种，其计数和运算都有共同的规律和特点。几种常用数制的比较见表1.1。其中，数码表示数的符号；基表示数码的个数；权表示每一位所具有的值。

表1.1　几种常用数制的比较

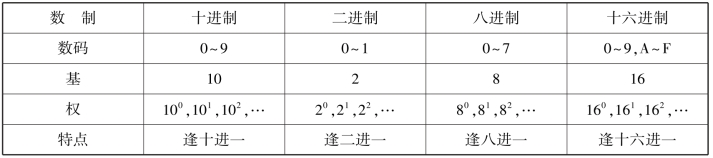
我们最熟悉、最常用的是十进制计数制，简称十进制。它是由0～9共10个数字组成，即基数为10。十进制具有“逢十进一”的进位规律。任何一个十进制数都可以表示成按权展开式。例如，十进制数95.31可以写成

（95.31）10＝9×101＋5×100＋3×10－1＋1×10－2

其中，101、100、10－1、10－2为该十进制数在十位、个位、十分位和百分位上的权。

二进制与十进制数相似，二进制中只有0和1两个数字，即基数为2。二级制具有“逢二进一”的进位规律。在计算机内部，一切信息的存放、处理和传送都采用二进制的形式。任何一个二进制数也可以表示成按权展开式。例如，二进制数1101.101可写成

（1101.101）2＝1×23＋1×22＋0×21＋1×20＋1×2－1＋0×2－2＋1×2－3

八进制的基数为8，使用8个数码即0，1，2，3，4，5，6，7表示数，低位向高位进位的规则是“逢八进一”。

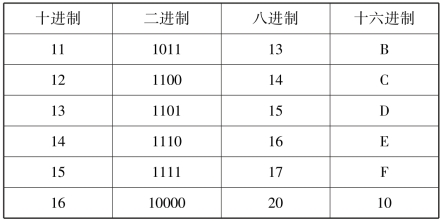
十六进制的基数为16，使用16个数码即0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F表示数。这里借用A，B，C，D，E，F作为数码，分别代表十进制中的10，11，12，13，14，15。低位向高位进位的规则是“逢十六进一”。常用的几种进位制对同一个数值的表示见表1.2。

表1.2　不同进制之间数字形式对比

续表

（2）数据的存储单位

位（bit）在计算机中最小的数据单位是二进制的一个数位。计算机中最直接、最基本的操作就是对二进制位的操作。我们把二级制数的每一位称为一个字位，或是一个bit。bit是计算机中最基本的存储单位。

字节（Byte）是一个8位的二进制数单元，也称为Byte。字节是计算机中最小的存储单元。其他容量单位还有千字节（KB）、兆字节（MB）、千兆字节（GB）、太字节（TB）及皮字节（PB）。它们之间有下列换算关系：

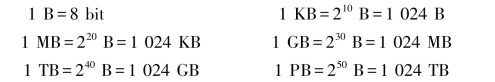
字是CPU通过数据总线一次存取、加工和传送的数据，一个字由若干个字节组成。而字长表示一个字中包括二进制数的位数。例如，一个字由两个字节组成，则该字字长为16位。字长是计算机功能的一个重要标志，字长越长表示功能越强。不同类型计算机的字长是不同的，较长的字长可以处理位数更多的信息。字长是由CPU决定的，如80286 CPU的字长为16位，即一个字长为两个字节。80386／80486微型计算机字长为32位，目前主流CPU的字长是64位。

一台微型计算机，内存为4 GB，光盘容量为700MB，硬盘容量为2 TB，则它实际的存储字节数分别为：

内存容量＝4×1 024×1 024×1 024 B＝4 294 967 296 B

光盘容量＝700×1 024×1 024 B＝734 003 200 B

硬盘容量＝2×1 024×1 024×1 024×1 024 B＝2 199 023 255 552 B

（3）常用数制的相互转换

①二进制数转换为十进制数。将二进制数转换为十进制数，只要将二进制数用计数制通用形式表示出来，计算出结果，便得到相应的十进制数。

【例1.1】　（1101100.111）2＝1×26＋1×25＋1×23＋1×22＋1×2－1＋1×2－2＋1×2－3＝64＋32＋8＋4＋0.5＋0.25＋0.125＝（108.875）10

②八进制数转换为十进制数。八进制数以8位基数按权展开并相加可以得到十进制数。

【例1.2】　（652.34）8＝6×82＋5×81＋2×80＋3×8－1＋4×8－2＝384＋40＋2＋0.375＋0.0625＝（426.4375）10

③十六进制数转换成十进制数。十六进制数则以16位基数按权展开并相加。

【例1.3】　（19BC.8）16＝1×163＋9×162＋B×161＋C×160＋8×16－1＝4096＋2304＋176＋12＋0.5＝（6588.5）10

④十进制数转换为R进制数。其中，整数部分的转换采用的是除R取余倒记法。(www.xing528.com)

【例1.4】　将（59）10转换为二进制数。

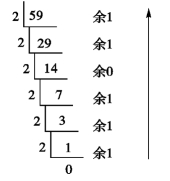
结果为　（59）10＝（111011）2

【例1.5】　将（159）10转换为八进制数。

结果为　（159）10＝（237）8

【例1.6】　将（459）10转换为16进制数。

结果为　（459）10＝（1CB）16

而小数部分的转换采用乘R取整法直到小数部分为0，整数按顺序排列，称为“顺序法”。

【例1.7】　将十进制数（0.8125）10转换为相应的二进制数。

结果为　（0.8125）10＝（0.1101）2

【例1.8】　将（50.25）10转换为二进制数。

分析：对于这种既有整数又有小数部分的十进制数，可将其整数和小数分别转换成二进制数，然后再把两者连起来即可。

因为　（50）10＝（110010）2，（0.25）10＝（0.01）2

所以　（50.25）10＝（110010.01）2

⑤R进制数之间的相互转换。

a.八进制数转换为二进制数：八进制数转换为二进制数所使用的转换原则是“一位拆三位”，即把一位八进制数对应于三位二进制数，然后按顺序连接即可。

【例1.9】　将（64.5）8转换为二进制数。

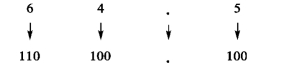
结果为　（64.5）8＝（110100.101）2

b.二进制数转换为八进制数：二进制数转换为八进制数可概括为“三位并一位”，即从小数点开始向左右两边以每三位为一组，不足三位时补0，然后每组改成等值的一位八进制数即可。

【例1.10】　将（110111.11011）2转换为八进制数。

结果为　（110111.11011）2＝（67.66）8

c.十六进制数转换为二进制数：十六进制数转换为二进制数的转换原则是“一位拆四位”，即把1位十六进制数转换为对应的4位二进制数，然后按顺序连接即可。

【例1.11】　将（C41.BA7）16转换为二进制数。

结果为　（C41.BA7）16＝（110001000001.101110100111）2

d.二进制数转换为十六进制数：二进制数转换为十六进制数的转换原则是“四位并一位”，即从小数点开始向左右两边以每四位为一组，不足四位时补0，然后每组改成等值的一位十六进制数即可。

【例1.12】　将（1111101100.00011010）2转换为十六进制数。

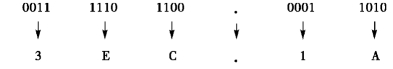
结果为　（1111101100.00011010）2＝（3EC.1A）16