物理学家的生活之轻松

这是当我看到摆时的情况。

从教堂高坛的天花板上，用一根长线悬挂着一个圆球，带着等时的庄严来回摆动。

我知道——但任何人能够感觉到它那种令人平静地呼吸的魅力——摆的周期受摆线长度的平方根和π支配，然而π这个数对尘世思想说是没有道理的。它通过较高度的相关性将一切可能的圆周与直径联系起来。圆球从这一端摆到另一端所花费的时间由最无时间性的量度之间神秘的巧合来决定：悬挂点的奇点性，平面维度的对偶性，由π开始的三因素，神秘的二次根性质，以及圆周本身数不完的完美。

——乌姆贝托·埃科^[23]

在你运用了一阵子的数学物理的方程式和公式之后，你就习惯于大自然的特殊性。请充分宽恕我们对某些细节的无知。大自然定律有几个组成部分：逻辑的手段用于从现在预测将来，在特定位置上，插进有关现在的精确信息，即特殊的大自然的常数，以及简单数字的集合。这些简单数字几乎在每个物理学的公式中与大自然常数一起出现。在第三章，我们看到爱因斯坦为伊尔斯·罗森塔尔-施奈德挑选出它们，并称它们为“基本常数”。它们正好都是数字。例如，一个钟摆的周期（“滴答”）高度精确地取决于一个简单公式：

这里L是摆的长度，而g是地球表面重力引起的加速度。注意出现的“基本常数”2π≈6.28。在我们用来描述物理世界的某些方面的每个公式中，都出现这类数字因子。值得注意的是，它们几乎总是相当接近于数值1，而且它们可以被忽略，或用1来近似，如果人们只对得到相当好的估计结果感兴趣的话。这是一个主要的额外好处，因为在诸如确定一个单摆周期的问题上，它允许我们找到近似的答案形式。具有时间量纲的周期唯一地取决于长度L和加速度g，按照某种方式组合导出的是时间：这个组合就是L/g的平方根。

物理世界的这个微妙特征，似乎可以用由数学定律作出美好的描述，定律中有纯粹数字的因子，其大小看来与1相差不很大，这是我们在物理世界的研究中几乎未被注意到的奥秘之一。爱因斯坦对在物理学方程中的小的无量纲数的普遍存在有很深刻的印象，并写下这奥秘，虽然这几乎总是事实如此，

我们不能要求对此作出严格的说明，为什么不应该有像（12π）³这样的数字因子出现在数学物理的推导中？但是这种情形无疑是凤毛麟角。^[24](www.xing528.com)

许多年之后，他在给罗森塔尔-施奈德的一封信中说对大自然的常数的这个奥秘被难住了：

问题似乎在于事物的本质上，即这类基本数字在大小量级方面与数字1没有不同，至少只要考虑局限于“简单的”情况，或依情形可能是“自然的”公式表述的情况。^[25]

如果我们认识到使爱因斯坦有如此深刻印象的几乎所有的数字因子都有几何学上的缘由，就有可能把这个问题搞清楚。例如，一个边长R的立方体的体积是R³，而半径为R的球体积是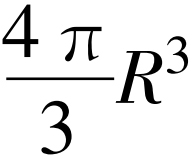。当大自然的诸力起作用时，数字因子允许具体形状有差别。由于大自然的诸基本力是球对称的，对于不同方向不会有任何偏爱，因此存在一种趋向于球对称的倾向。像这样的观测使我们只能提供爱因斯坦关于他的问题的一个可能的答案。

我们知道半径R的圆的周长为2πR。圆球的表面面积为4πR²。同样，圆的面积是πR²，球的体积是4πR³/3。现在想像在N维空间中的“球”。数学家们能容易地算出这类球的面积和体积是多少。很显然，半径R的N维球的面积为A(N)，应正比于R^N-1，而它的体积V(N)正比于R^N，但根本不明白像“4π”或“4π/3”类似的数字会是什么。这些公式见图10.10中的曲线。

图10.10　半径等于一个单位长度的N维球体的表面积和体积随半径发生变化。体积在N近5.3处有一个极大值但随后急速下降。

这个图值得注意的特征是，随着空间维数增加以至数字因子增大，变得大大异于1。它们并不按与N成正比地增长，或甚至也不按2^N增长。它们按N^N的方式增长。所以，我们对爱因斯坦有一个答案。大自然的定律中小的数字因子和物理学公式两者的普遍性是这世界的空间维数为很小的数的结果。如果我们生活在有20维的世界里，那么忽略物理公式中的数字因子的简单估计在许多情况中会极端地不正确，而爱因斯坦会问为什么它们总是大得如此不方便。

从这里，我们看到大自然的常数在确定三维空间中大自然定律的结果时会比它们在更多维度空间的宇宙中起的作用有更大得多的相对影响。