毕达哥拉斯与数字占卜术：数值之谜

这里躺着约翰·邦，

使他丧命的是一杆枪，

他的名字不是邦（Bun），而是伍德（Wood），

但是伍德（Wood）与枪（gun）不押韵，

而邦（Bun）才押韵。

——墓志铭^[15]

吉利的数、不吉利的数、特别的数——许多百姓认为他们能指望这些数。这是古代迷信的一种现代残余。如果我们回顾公元前约550年，我们发现毕达哥拉斯和他的希腊门徒们为了其自身缘故对数学进行了某些最早期的研究。他们对宇宙中的每一件事物都有兴趣，把它们归因于数。这是将世界上这些不相干的部分联系一起的一种方法，将行星的运动编成音乐的音阶，且将物理量转化为几何学图形。不像我们，他们并不认为数字只是事物的属性。他们认为每件事物就是一个数。数字有它内在的意义。它们并不只是事物之间的关系。出于这些虔诚的信念，接下来是以各种可能的方法寻求探索事物的数，查找这一个生活领域中的数与另一领域的数之间重合的关系。某些数具有好的特征，其他数则不太吉利。某些数需要保守秘密，其他数则可以公之于众。

为了搞清楚怎么会导致毕达哥拉斯对数字占卜术有强烈的信念，我们就应考察他喜欢用数字玩的某些游戏。他的喜好之一是三角形数字系列。在这里我们可以看到，一旦在地上摆上细卵石或棋子等其他点状物，一张简单的数字图就相当自然地出现了。如果我们将一、二、三……个点状物相继摆在每个前排下面，那么我们就构成一个数字的级数。这些数呈“三角形”的形式（见图4.3）。

图4.3　三角形的数是由排在下一排的点比上一排多一个点产生的。^[16]

将它们逐步加起来形成三角形数字的级数：

1，1+2=3，1+2+3=6，1+2+3+4=10，等等。^[17]

对于毕达哥拉斯的信徒们来说这是一个特别有启发性的例子，因为希腊人是用他们的字母表中的字母来表示数字的，这样就使我们本来一目了然的系列数的图形变得晦涩费解，用毕达哥拉斯的图形表示三角形的数是令人着迷的。的确，今天当我们称数字为“图形（figure）”时，我们就记起了它。figure仍然带有两重意义：图形和数字。由此得到1的图形是一个点，2是两个点相连的线，而3是一个三角形，第一个围成一个区域的平面图形。数字4则用第一个立体图形表征，由四个三角形面组成的金字塔有四个角顶。

按同样的方法，就有可能说出“平方”数： 4，9，16，25，……它们可由点子排成的方形阵列来构成。另一种方法是人们注意到，平方数可由相继的奇数相加来构成，例如，^[18]

4=1+3

9=1+3+5

16=1+3+5+7

25=1+3+5+7+9

36=1+3+5+7+9+11

这些例子说明毕达哥拉斯是如何被吸引作出他的第一次富有想像力的飞跃，并认为数字是事物——几何学的客体。其次，他作出了一个甚至更令人难忘的发现。他注意到希腊乐器的音调依赖于简单的数字之比，1∶2，3∶2，4∶3和8∶9。这些是希腊人认为的谐音并最悦耳的唯一的音程。这个发现对毕达哥拉斯思想的影响是深远的。他认为他已经发现人类感知的变化依赖于数学。更有甚者，在描述音程和行星运动方面出现相似的数字令毕达哥拉斯学者坚信这些表面上各不相同的现象是有内在联系的。

什么是数字占卜术的基础呢？它是一种信念，相信存在着与数字本身有关的某种有内在意义的东西；相信7是一个具有共享性质的数，它将具有七重特性的所有事物联系在一起，不管他们是7位新娘和7位兄弟，还是一个礼拜有7天。对于某些数字来说则要小心，如13，被认为是不吉利的，或其他数，如7，被认为是吉祥的。毕达哥拉斯学派赋予某些数字具有特殊的属性，如良好或正义。在许多方面而不止一个方面，它们变成了符号。这里有一则典型的评论：

由于他们假设正义、报答或平等有确定的特性，并发现这就存在于数字之中，因此他们说正义是第一个正方形数，适合各种类型，具有相同公式的第一例事物。按他们的意见，要给它一个最恰当的名字。这个数有人就称之为4，作为第一个正方形，将它分成相等，且各种分法都相等，对此就是2的两倍。然而，其他数，譬如说9，它是一个奇数的第一个平方，即3乘它本身。

另一方面，他们说与幸运有关的数是7，因为本质上与出生和成熟有关的各个完成日期都依照7的倍数发展。以男人为例子，他可能在母亲怀孕7个月之后出生，之后又7个月长出他的新牙，大约在第二个7年期末到达青春期（即14岁），而在第三个七年期末长出胡须。^[19]

某些数特别受到尊敬，因为它们有特殊的性质。所谓的“完全”数是因为他们有明显的特性，它们等于正好能整除它们的所有数之和，除它们本身之外。第一个完全数是6=1+2+3；第二个是28=14+7+4+2+1。下两个是496和8 128，而且早期希腊人也知道它们。即使在今天，人们所知道的完全数也只不过33个，^[20]没有人知道完全数是否有无限多个，如同素数那样。^[21]

毕达哥拉斯也对他称之为“友好数”的一连串数有很深刻的印象。如果第一个数的除数之和等于第二个数，反之亦然，则这两个数就称为“友好数”。在某种意义上，它们被判定为具有同一个“父母”，神职人员更喜爱用这些成对的友好数记东西。例如220和284就是友好数。^[22]你可用1，2，4，5，10，11，20，22，44，55和110来除220。将它们加起来你就得到284。你可用1，2，4，71和142来除284。将它们加起来便得220。早期犹太学者非常喜欢用数字占卜术来批准他们手稿的正文或抽取它们所包含的各个量背后某些更深藏的意义。^[23]这种崇敬演化成为最极端形式的希伯来神秘主义，以体现它的对七重事件的崇敬。这里有一则医治疟疾的数字占卜术的另类药方：

从7棵棕榈树上摘来7颗果实；从7道梁上取来7片木屑；从7座桥上取来7根钉子；从7只火炉中取出7把灰；从7个门臼里取出7勺土；从7艘船上取来7枚松脂，7小撮土茴香；从一条老狗身上拔下7根颔毛，并把它们结在带有白色捻线的衬衫的领孔上。^[24]

最“神圣的”毕达哥拉斯数是头四个数： 1、2、3和4，它们生成的三角形数是10（见图4.4）。

图4.4　神秘的四底“毕氏图”（tetradktys），代表数字10（为1+2+3+4）的三角形。

这个代表数字10的三角形是神秘的四底“毕氏图”的符号，新进入毕达哥拉斯社团的信徒要用它发誓保密和忠诚。作为他们的加入社团条件的一部分，他们要宣誓保密三年，而结果在文艺复兴时期三年的总天数（3×365=1 095）被用作为静默的数字。这四底“毕氏图”只不过是一把总钥匙，用来开启我们对整个生命和经验的理解。这里列出公元一世纪时的一位评论家关于四件事的十个集锦，相信它是具有象征性意义的： ^[25]

数： 1、2、3、4。

大小：点、线、面、立体。

简单物体：火、空气、水、地。

简单物体形状：金字塔、八面体、二十面体、立方体。

生命物体：种子、沿长度、宽度、厚度生长。

社会：人、乡村、城市、国家。

才能：推理、知识、意见、感觉。

一年四季：春、夏、秋、冬。

年龄：幼年、青年、成年、老年。

人的要素：身体和灵魂的三要素。

这些奇妙的观念有异乎寻常的持续性。每个年代，每个地方，都有一些作家和思想家痴迷于数字的含义。他们对待方程式和公式好像它们就是将宇宙的真正意义包于囊中的神秘密码。在今天，这种观点也不会灭绝。虽然我们用数学建立了事物之间的关系，仍然有大量业余研究爱好者不断寻找特殊的“公式”来告诉人们有关物理学世界的终极本质的某些东西。而且认为这个公式能告诉我们的东西优于处于物理学真实核心的那些数：大自然的常数的数值。数字占卜术已经把它的注意力转到大自然的物理常数，试图用π、平方根和普通数的一连串的联系来解释它们的数值。

这些努力靠巧合过日子。某些给人以最深刻印象的数根本没有什么看得出的意义。例如，^[26]有人曾经提出

精确到三亿分之一！或者在1859年查尔斯·埃尔米特⁽¹⁾第一次宣布：数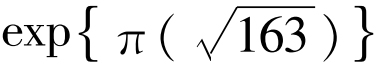是一个整数，你以为如何。现在知道这个数非常接近于：

262 537 412 640 768 743.999 999 999 999 999 25……

这列出的部分出自马丁·加德纳对4月愚人节的戏弄，他宣称这个数是一个整数，且印度数学家拉曼纽扬（Ramanujan）已作出预言它是整数。^[27]结果，它就变成称为“拉曼纽扬常数”。

但是存在着惊人之多的数字以及更多的它们的各种可能排列。巧合的情形似乎比较显著，因为我们不会去考虑，我们在发现这些数期间遇到了多少没有给人什么印象的“非巧合的情形”。当我们从统计学的观点来分析时，能证明像这样的巧合事件并非是异乎寻常的。人们记得当尤利·格勒在电视上露面宣布他要使你家里的时钟停下来时，有几百万观众和我们期盼大量上紧发条的时钟像他所讲的那样停下来。那些有钟停走的家庭对此有极深刻的印象。其余人只是想他们不会是心灵上听腻了！总之，他真的使其他许多时钟停了。

我所喜爱的数字巧合是我的一个文学朋友斯蒂芬·梅德卡夫告诉我的一个有关例子，该例子是反对任何试图评价靠运气出现的数字符合的数学上的可能性。我想起大约七十年前一位伊顿公学的男学生提出注意的事。首先，我没有能力来判别这一背景。这里有一个传统或传说，威廉·莎士比亚参与了詹姆士国王钦定版的英文《圣经》中“诗篇”的某些英文翻译。^[28]有人指出莎翁的手可察觉到“诗篇46”，莎士比亚在46岁那年译写这诗篇。因为如同这位男学生指出的，该诗篇从头数起的第46个词是“shake”^[29]。从最后倒数第46个词是“spear”（连在一起Shakespear，即莎士比亚——译者注）是巧合还是暗存玄机？

所有各种各样的结合大自然的常数的某些数值的数字巧合都可以在科学文献中找到。而更多的是在物理学家们的文件筐中找到，那里是本意良好的记者到达的地方。这里有一些针对精细结构常数提出的公式（没有一个公式是严谨取得的）。将它们与最佳实验值作比较：

实验值：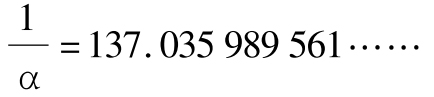

首先，有一些人试图利用已知的物理学知识的猜测性推广来“证明”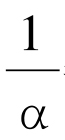等于下列表示式：

刘易斯和亚当斯^[30]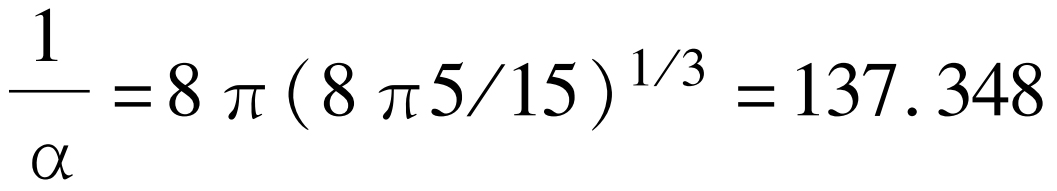

爱丁顿^[31]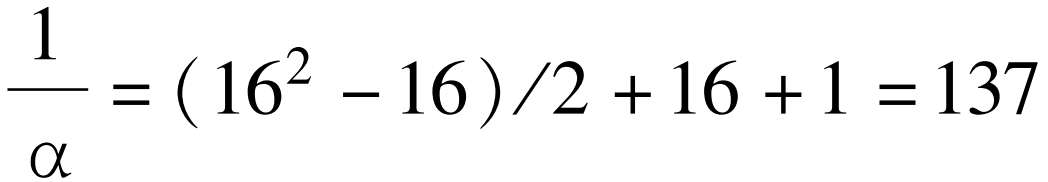

怀勒^[32]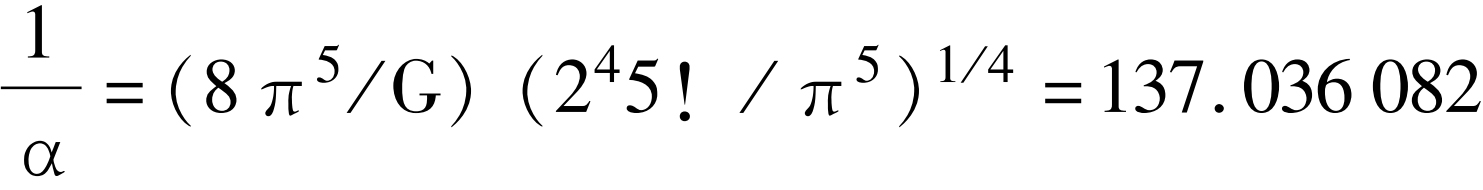

阿斯普登和伊格尔斯^[33]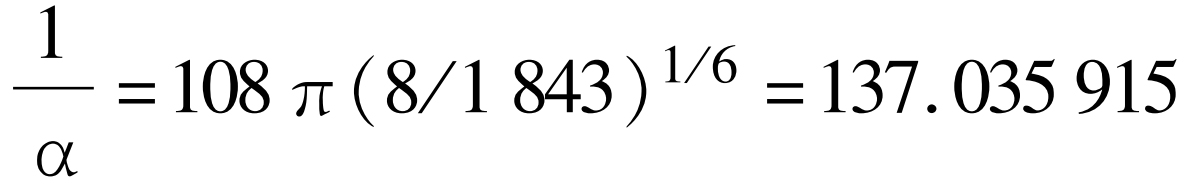

当然，如果M理论最终出现可确定的1/α的数值，它可能看上去颇像这些猜测的公式之一。可是，它会提供一座宏大而连贯的理论大厦由此导出这预言。它还需要作出某些有关我们尚未测量的事物的预言，例如1/α的下几位小数值，以便未来的实验者能够寻找它，检验它。

所有这许多件的数字技巧活动给人很深刻印象，这是因为它们接近于实验值（在过去当它们第一次被提出来时，甚至更接近实验值），但是不断地别出心裁的奖项应该授予加里·亚当森，^[34]他的137-专门学的淘气鬼画廊见图4.5。

图4.5　加里·亚当森编辑的涉及数字137的某些数字占卜术的奇思妙想。

这些例子至少具有显示来自对电磁学和粒子理论的某种意图的功能。但是也还存在若干“纯粹的”数字占卜术学家们寻求任何小数的幂次项和重要的数学常数如π的幂次项组合，得出接近于所需要的数值137.035 989 561……这里有几个这类的例子：

罗伯特森^[35](www.xing528.com)

伯格^[36]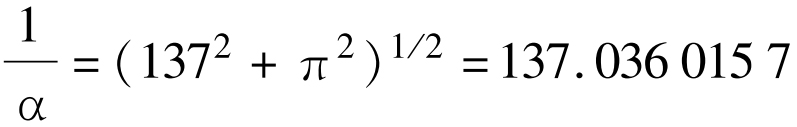

甚至伟大的理论物理学家沃纳·海森伯（Werner Heisenberg），抵挡不住厚脸滑舌的嫌疑说^[37]：

至于数值我猜想1/α=2⁴3³/π，但是那当然是个玩笑。

有太多的数字占卜术，等一会儿它就开始上瘾了。搞清楚，为什么在世界范围有如此持久的对数字占卜术的迷恋是容易的。我们的目的是揭示某些例子并不是没有正经的对象。我们上面所列的公式之一，带有阿瑟·爱丁顿（Arthur Eddington）的名字，他是20世纪最伟大的天体物理家之一。在下一章我们将更密切关注爱丁顿。他是一位将学识渊博与奇思妙想结合起来的非凡人物。超过任何一个现代人，他要对发动永无止境地试图用纯粹数字占卜术的技巧来阐明大自然的常数的运动负责。他也关注大自然的常数的新的和令人激动的特点。

注释

[1]　克里斯（R. P. Crease），“物理学和政治学混合了吗？”载《物理世界》，2001年2月，第17页。

[2]　引自皮柯弗（C. Pickover），《上帝的灵影》，普莱纳姆出版社，纽约，1997，第26页。

[3]　巴罗（J. D. Barrow），《发现自身的宇宙》，牛津大学出版社，1990，更加详细地讨论大自然的“定律”概念的发展。

[4]　我们不期望大自然的定律的每一个可能的结果在现实中都存在。因此实际的世界是一切可能世界的一个子集。一个有意义的问题是关于反对某个世界其中在定律的结果方面存在逻辑的不协调一致但它们并不声称有任何实际结果。

[5]　引自保罗斯（J. A. Paulos），《我思考，因此我笑》，哥伦比亚大学出版社，1985，第35页。

[6]　参见，例如，现代重印的G·伽莫夫，《托普金斯先生》平装本，剑桥大学出版社，1949。最新增订版，托普金斯先生的某些教育经验可以在罗素·斯坦纳德的编辑工作找到。

[7]　光速是1676年由丹麦天文学家欧拉夫·卢默（Olaf Roemer）首先卓越地导出。他注意到木星的几个卫星中一个月食之间所经过的时间间隔，当地球从木星离开时此时间间隔增长。而当地球趋近木星时间隔缩短。他发现在经历一年做的许多观测得到月食之间的平均时差为996秒。卢默于是把这时间差归因于光具有有限速率的事实。因此他认为光穿过等于地球轨道直径的距离必需的时间为996秒。这个距离是知道得很精确的，即使那时，也允许他得到光速的一个极好的估计值。

[8]　伽莫夫，《托普金斯先生》平装本，第1页。

[9]　伽莫夫需要允许在这里有某种艺术的破格。如同我们在最后一章中解释的那样，仅仅改变有量纲的大自然的常数，如光速，不会导致世界的行为有任何观测上的差异，如果其他常数也改变以至一切无量纲的常数保持同一数值的话。

[10]　h有非零的数值对于物质的稳定性是重要的。如果一个原子的能量可以按任意小量来变化，那么所有原子会很快变得极不相同。其他原子的冲撞和辐射会在任何时间改变它们的能级。常数h足够大，原子在它们被撞进第二个许可的能级之前需要有一个相当大的“冲击”。

[11]　根据L·B·欧昆（Okun）说，这些常数的这种表示是俄罗斯物理学家马特维·布龙斯泰因早在20世纪30年代引入的。布龙斯泰因不幸被斯大林杀害于1938年，当时他只有32岁。有一本传记（俄文）出自G. E. Gorelik和V. Ya. Frankel，《马特维·彼特罗维奇·布龙斯泰因》，Nauka， Moscow，1990。

[12]　大卫·辛马斯特（David Singmaster）的报告收在施特本和桑福德（M. Stueben and D. Sandford），《黑板前面二十年》，美国数学学会，华盛顿，1998，第95页。

[13]　至今还不可能预言最后一次爆炸后会遗留下什么东西。曾经提出过许多不同的建议，从根本不留下什么，到在空间和时间中留下一个空洞，一个虫洞进入一个新的宇宙，或者只有一个稳定的质量。

[14]　我们不知道，例如，精细结构常数是有理数呢还是无理数。

[15]　威尔逊（D. M. Wilson），《令人敬畏的结局：大英博物馆墓志铭集》，大英博物馆出版社，伦敦，1992，第82页。

[16]　巴特勒（C. Butler），《数字符号论》，劳特利奇-基根·保罗出版社，伦敦，1970。

[17]　第n个三角形数等于n（n+1）/2。

[18]　一般来说，n²等于头n个奇数之和，起始为1。

[19]　亚历山大的阿佛洛狄西亚斯（亚里士多德的一位评论家）在他的《形而上学》，38，10引自格思里（W. Guthrie），《希腊哲学史》，卷Ⅰ，剑桥大学出版社，1962，第303—304页。

[20]　一切完全数可表示为2^N （2^N+1-1）这里N为特殊的数值。伟大的瑞士数学家里昂纳德·欧拉证明所有偶数的完全数（perfect number）具有这个形式。如果2^N-1是素数。没有人知道是否存在奇数的完全数。

[21]　素数如7和23，除了本身和1之外没有除数。欧几里得以一个极美妙的论证证明素数有无限多个。假设它们只存在有限个。将它们相乘在一起再加上1。那么这个数不可能被你所取的有限的素数表中任一素数除尽因为总有余数1。因此这个数要么是一个素数或者它是能用比你的原始表里最后一个更大的素数除尽。不管是什么情况，这与原始假设素数表是有限的是矛盾的。所以素数的数目不能是有限的。

[22]　已经发现大于一千的友好数（amicafle numbers）。下一个最大的是1 184和1 210，2 620和2 924，5 020和5 564，6 232和6 368，10 744和10 856。

[23]　在《创世记》，第32章，14节，友好数220出现于雅各给以扫220只山羊的礼物。这意含一种关系保证会有回赠的礼物284件。

[24]　特拉赫滕贝格（Trachtenberg），《犹太人魔法和迷信》，载皮柯弗（C. Pickover），《上帝的灵影》，普莱纳姆出版社，纽约，1997，第80页。

[25]　士麦那的神，关于四底“毕氏图”和死亡，引自C·巴特勒，《数字符号论》，伦敦，劳特利奇-基根·保罗出版社，1970，第9页。

[26]　韦伯（H. Weber），《代数教科书》，卷3，切尔西出版社，纽约，1908，第125节。这个例子引自古德（I. J. Good）未发表的资料，统计学系，弗吉尼亚工学院，技术报告，《物理学的数字占卜学》，1988年12月30日，第1页。

[27]　这是四月愚人节骗局的部分内容，刊载《科学美国人》1975年4月版第127页马丁·加德纳专栏中。（这个骗局披露于1975年7月刊，第112页）。某人能证明存在某些有理数等于一无理数自乘一个无理幂，但据我所知，没有一个明显的例子被说明。其证明是一个漂亮的非一结构性的证明例子。考查数x等于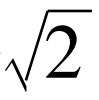自乘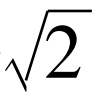次幂。这个数要么是有理的或是无理的。如果是有理的，正是我们要寻找的，所以假定它是无理的。再将它自乘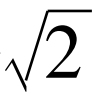次幂，我们得，它是有理数并等于一个无理数自乘一个无理数次幂，真的依照假设！

[28]　这钦定版本是1604年汉普顿宫廷会议的结果，这个会议是詹姆士一世召集的，它把各种高教会派和低教会派合在一起。这个结果“钦定版本”（虽然它实际上根本不是任何官方方式意义上“经授权的”）出现于1611年。它大部分是根据威廉姆·丁多尔的翻译文本，用的资料来自约翰·威克利夫。威廉姆·莎士比亚生活年代由1546年到1616年。

[29]　《圣经·诗篇》第46首第一节和最后一节读出（从开始和最后数起第46个词是大写体！）

神是我们的避难所，是我们的力量，

是我们在患难中随时的帮助。

所以地虽改变，

山虽摇动到海心；

其中的水虽砰訇翻腾，

山虽因海涨而战抖，

我们也不害怕。

……

他折弓，断枪，把战车焚毁在火中，

“你们要休息，要知道我是神：

我必在外邦中被尊崇，在遍地上也被尊崇。”

万军之主与我们同在；

雅各的神是我们的避难所。

[30]　 G. N. Lewis and E. Q. Adams. Phys. Rev. 3.92（1914）.

[31]　阿瑟·斯坦利·爱丁顿，《皇家学会论文集》，A 122，358（1930）。注意在这时爱丁顿相信1／α是一个整数。此时这是在其测量上实验的不确定程度给出的一种可能性。

[32]　 A. M. Wyler, C. Rendus, Acad. Sci., Paris B 269, 743 （1969） and B 271, 186（1971）.

[33]　 H. Aspden and D. M. Eagles, Phys. Lett., A 41, 423（1972）.

[34]　皮柯弗（C. Pickover），《计算机和想像力》，圣马丁出版社，纽约，1991，第270页。

[35]　 B. Robertson, Phys. Rev. Lett., 27, 1545 （1971）.

[36]　 T. J. Burger，Nature 271, 402（1978）.

[37]　 W·海森伯给保罗·狄拉克的信，1935年3月27日，引自克拉格（H. Kragh），《狄拉克：科学的生涯》，剑桥大学出版社，1990，第209页。

（1）　埃尔米特（Charles Hermite， 1822—1901），法国数学家。——译者