普通物理学中的X射线产生机制解析

6.9.1 结构图

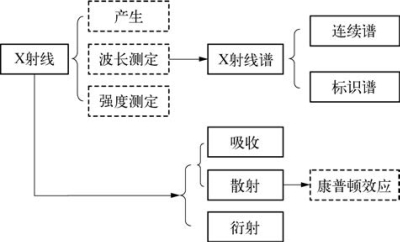
6.9.2 X射线的产生与测定

1.X射线又名伦琴射线,是一种波长较短的电磁波。

2.通过对X射线的研究,使我们对原子结构有了进一步的了解。

3.X射线产生:用高速的电子打击物体。

如图6-25所示,K是钨丝做成的阴极,A是阳极(又称靶子),高压电源一般是几万伏到二十几万伏。K发射的电子被电场加速后打在A上,就有X射线从A发出。

X射线是人眼看不见的光,但能使照相软片感光。其波长很短,约在0.1nm或更短。

图6-25 X射线的产生

4.X射线波长测定

如图6-26所示,发出的X射线先后穿过两块铅板的窄缝S1和S2,形成一束光线,射在晶体C上。P是照相软片,围成圆弧形,圆心在晶体C处。

慢慢转动晶体C,当转动到某一角度θ时,即满足布拉格方程:

nλ=2dsinθ(n=1,2,3,…)

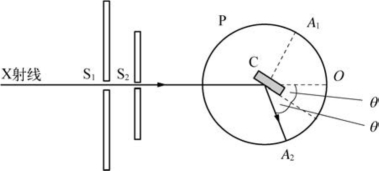
图6-26 X射线波长测定

式中,d为晶体C中原子各组平面之间的距离。此时,射线中就有光线射到A2处。

多次转动晶体C,得到与A2对称的A1,得到4θ的大小,再计算得到d的数值,就可以得到X射线波长λ。

5.X射线强度测定(略)

6.X射线谱

(1)连续谱

在波长连续变化的波谱中:

式中,λ0为最短波长;ν0为最短波长的频率;V为外加电压;Ve为电子达到靶子的动能。

分析:①连续谱是电子在靶子上被减速产生的。

②高速电子打到靶子上后,受原子核中库仑电场作用而骤然减速,电子的动能转化为辐射能,有射线放出,这种辐射能称为韧致辐射。

③如果电子深入靶子的深度不同,能量的损失就有各种数值,呈现的波长是连续变化的。

④如果电子被停止,全部能量转化成辐射能,发射的一个光子的能量就等于电子的动能。

⑤计算获得的最短波长:

(2)标识谱

①每一种元素都有一套一定波长的射线谱作为这种元素的标识,所以称为标识谱。

②各种元素的标识谱有相似的结构,分成几个线系。波长最短的一组线系称为K线系,一般可以观察到三条谱线:Kα、Kβ和Kγ。

③还有L线系(波长较长)、M线系和N线系(波长更长)。

④莫塞莱定律:描述Kα谱线

式中,Z为原子序数;R为里德伯常数。

⑤X射线的标识谱是靶子中的原子内层电子跃迁发出的;K线系是最内层(n=1)以外各层的电子跃迁到最内层的结果;L线系是第二层(n=2)以外各层电子跃迁到第二层的结果;M线系是第三层(n=3)以外各层电子跃迁到第三层的结果。n=1,2,3,…分别称为K层、L层、M层……各层电子分别称为K电子、L电子、M电子……

⑥标识谱反映了原子内层结构的情况。

⑦标识谱的获得方法

根据泡利原理,因为各层电子都是填满的,所以不可能有电子跃迁发生。如果要发生跃迁,那么某层电子必须产生空位。产生空位的方法有两种。

方法一:利用高速电子撞击原子,使它发出射线,即产生X射线。

方法二:把研究材料放在另一条射线发出的路径中,发射次级射线。

产生跃迁的选择定则:

ΔL=±1;

ΔJ=0,±1(www.xing528.com)

式中,L为能级;J为总角动量量子数。

6.9.3 X射线的吸收和散射

X射线在经过物体后强度减弱是由以下两种过程导致的。

1.吸收

(1)射线强度减弱

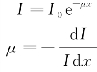
式中,I0为没有放入吸收物之前的射线强度;I为放入吸收物之后的射线强度;μ为衰减常数;x为吸收物厚度。

(2)应用

①利用X射线的高穿透性检查物体内部。

②研究原子内层结构。

2.散射

(1)射线方向改变,在原方向强度减弱。

μ=τ+σ

式中,τ为真实吸收系数;σ为散射系数。

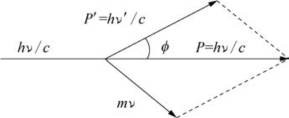
图6-27 康普顿效应

(2)康普顿效应:部分光线的波长变长,如图6-27所示。

式中,λ'为散射后波长;λ为散射前波长;h为普朗克常量;m0为电子静止时质量;c为光在真空中的传播速度。

分析:波长的变化只与散射角ϕ有关。当ϕ=90°时,

(3)综合

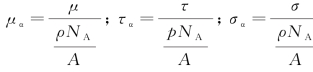
式中,μα为原子衰减常数;τα为原子吸收系数;στ为原子散射系数;ρ为吸收物密度;NA为阿伏伽德罗常数;A为原子量。μα、τα和σα分别代表射线经过单位截面只有一个原子的一层吸收物后被减弱、吸收和散射的百分数。

6.9.4 X射线的衍射

1.晶体是原子有规则排列起来的结构,这种有规则的排列沿各方向是作等间隔重复的。一个晶体可以看作是多个基本单元的联接。

2.一般而言,晶体的基本单元可以用一个平行六面体代表,这个六面体的三个边长是a、b和c,三边不一定相互垂直。

如果用坐标系来表示,设x轴在a的方向,y轴在b的方向,z轴在c的方向,如图6-28所示。

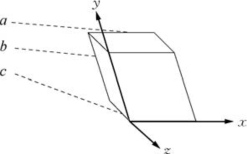
图6-28 X射线的衍射

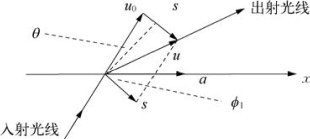
图6-29 立体光栅作用

3.当一束不同波长的射线射入晶体时,晶体对X射线起了立体光栅的作用。

如图6-29所示,在x方向,u0和u是入射方向和出射方向的矢量,s=u-u0 |s|=2sinθ。通过推导,我们得到布拉格公式:

nλ=2dsinθ (n=1,2,3,…)

式中,d为晶体中原子各组平面之间的距离。

在x、y、z三个方向上,

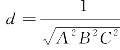
式中,A=h/a;B=k/b;C=l/c;h、k和l称密勒指数。

对于正立方晶体,因为三轴相互垂直,而且a=b=c,所以:

4.应用

(1)劳厄相片:利用X射线分析晶体结构。

(2)晶体粉末法:使用粉末代替上述晶体。