量子力学初步-普通物理学知识结构分析

6.4.1 结构图

按电子的轨道运动来描述原子结构具有一定的成就,但是存在局限性,而量子理论的研究为之开辟了一条新的路径。

6.4.2 光的二象性

1.光的波动性:光的干涉、光的衍射和光的偏振。

2.光的微粒性:黑体辐射和光电效应。

(1)一个光子的能量

E=hν

式中,h为普朗克常量;ν为光的频率。

(2)一个光子的质量

根据相对论原理,能量和质量的联系为:

式中,c为真空中的光速。

(3)一个光子的动量

式中,k=1/λ,k即光谱中的波数ν～。

6.4.3 物质的二象性

1.德布罗意推想:光有波动性和微粒性,实物粒子如电子、质子等是否也有二象性?

2.比较

实物粒子的动量:

P=mv

光子的动量:

3.德布罗意波:同实物粒子联系的波。

式中,λ为波长。

4.德布罗意波的实验

如图6-10所示,G为电子源,电子加速后从小孔发射,形成电子束,打在晶体T上,C是接收器,根据加在电子上的加速电压V,可以计算波长:

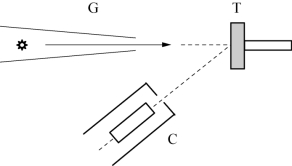
图6-10 德布罗意波实验

如果电子确有波动性,电子束射在晶体上就像光一样会发生衍射。

5.测不准原理

(1)在经典力学中,粒子的运动状态是用位置和动量来表示的,在任何时刻都可以准确测定。

(2)由于物质的波粒二象性,要同时测定物质的位置和动量是相当困难的。

(3)如果要非常精确地测定粒子的动量,即Δp→0,那么位置就非常不确定,即Δq→∞;反之,要精确测定位置,动量就非常不确定。

(4)同时测定粒子的位置和动量的极限:

式中,h为普朗克常量。

同理,同时测定粒子的能量和时间的极限:

(5)测不准原理来源于物质的二象性,因此测不准原理是物质的一个客观规律。

6.波函数

(1)电子(实物粒子)的波动性:波的前进方向就是电子的前进方向。

(2)用物质波的波函数(Ψ)形式描述微观粒子的运动状态:

上式表示一个质量为m、动量为p、能量为E、沿x轴运动的自由粒子的波函数。波函数是时间和空间(坐标系)的函数。

(3)根据物质波的频率和波长与粒子的能量和动量之间的关系,根据E=hν,p=h/λ及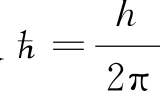得:

(4)物质波的波函数是一个复数形式,它本身不代表任何可观察的物质量。(www.xing528.com)

(5)波函数的统计意义:在空间某处的波函数Ψ的平方代表t时刻粒子在该处单位体积中出现的概率。

(6)波函数的归一化条件:粒子在空间各点出现的概率总和必等于1。

7.薛定谔方程

(1)波函数是描述粒子的运动状态。

(2)薛定谔方程是描述粒子的运动规律。

①含时薛定谔方程:考虑时间t和坐标(空间)x。

质量为m的粒子在外力场中运动,势能V为坐标和时间的函数。

在一维情况下的方程解:

②定态薛定谔方程:只考虑坐标(空间)x,与时间t无关。质量为m的粒子在外力场中运动,势能V仅为坐标的函数。

(3)薛定谔方程的应用

①一维无限深势阱中的粒子

在一定条件下,电子在金属中运动的势能曲线的形状与陷阱相似。势能分布如图6-11所示:

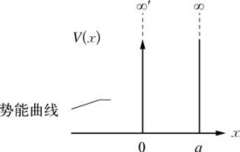
图6-11 势能曲线

式中,En为粒子能量;整数n为粒子能量的量子数;粒子在宽度a范围内运动。

②一维方势垒(隧道效应)

势能分布如图6-12所示:

③应用于氢原子的四个量子数

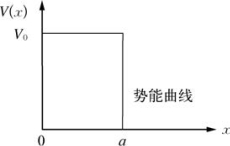
图6-12 一维方势垒势能曲线

ⓐ主量子数n:原子的能级是量子化的。

式中,E为能量;n=1,2,3,…,n。E与n2成反比。

ⓑ角量子数l:角动量也满足量子化条件。

式中,L为角动量;l=0,1,2,…,(n-1)。

ⓒ磁量子数ml:

式中,Lz为角动量分量(z轴);ml=0,±1,±2,±3,…,±l。

ⓓ自旋磁量子数ms:

自旋角动量S:

式中,sz为自旋角动量S的分量(z轴);m的可能值只有。

④小结

(a)通过这四个量子数,可以确定电子在多电子原子中的分布。

ⓐ主量子数n:决定电子的能量。

ⓑ角量子数l:决定电子在核外运动的轨道角动量。

ⓒ磁量子数ml:决定轨道角动量在特定方向上的分量。

ⓓ自旋磁量子数ms:决定自旋角动量在特定方向上的分量。

(b)泡利不相容原理:任何两个或两个以上的电子,不可能有完全相同的一组量子数。

(c)能量最小原理:在原子系统内,每个电子趋向于占有最低的能级,从最内层开始向外排列,整个原子的能量最低,原子处于最稳定的状态(基态)。