原子光谱与能级分析-普通物理学知识结构分析

6.3.1 结构图

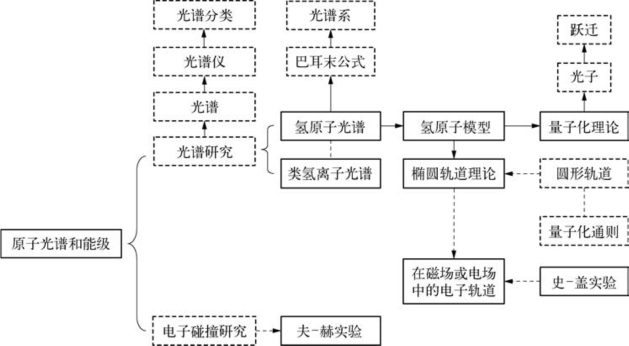
6.3.2 光谱研究

1.为什么要研究光谱?

原子的核式结构只肯定了原子核的存在,但不能确定核外电子的情况,对光谱的观察,为我们提供了关于这方面许多有价值的结果。

2.光谱:描述光波(电磁波)的波长和强度。

3.光谱仪:描述光谱的仪器,在相片上形成一系列的实像(细线),以判定光波的波长和强度。

4.光谱分类(如图6-2所示)

图6-2 光谱分类

(1)线状光谱:由原子发出的光谱。

(2)带状光谱:由分子发出的光谱。

(3)连续光谱:由固体加热后发出的光谱。在某些情况下,原子和分子也会发出。

5.氢原子光谱

(1)从氢气放电管可以获得氢原子光谱。

(2)巴耳末公式

式中,λ为波长;B=364.56nm;n=3,4,5,…

如果令1/λ=ν～(波数),公式改写为:

式中,RH称里德伯常数,RH=1.0967758×107m-1;当n→∞时,ν～表达线系限的波数。

(3)氢原子光谱系

式中,m=1,2,3,…对应的n=2,3,4,…,当n=2,3,4,…时,为赖曼系;当n=3,4,5,…时,为巴耳末系;当n=4,5,6,…时,为帕邢系;

……

图6-3 玻尔氢原子模型

式中,T称光谱项。氢原子光谱项:普遍等于,n=1,2,3,…

(4)玻尔氢原子模型

图6-3中,一个带负电荷的电子e,质量为m;一个带正电荷的原子核Ze,质量为M。电子围绕原子核旋转。

①向心力

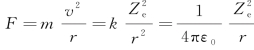
式中,r为电子与原子核之间的距离,即原子半径;v为电子绕原子核转动的速度;k为玻耳兹曼常数,k=1.38062×10-23J·k-1。

②原子内部能量

ⓐ电子动能:

ⓑ体系势能:

ⓒ原子内部能量:

式中,总能量是负的,表示要把电子从原子中移开必须对电子做功。

③电子轨道运动频率

(5)量子化理论

经典电动力学理论无法解释原子光谱的不连续性。用量子化理论解释如下。

①光能量是一个单元的整数倍,每一个单元能量是hν。其中,h是普朗克常量,h=6.62620×10-34J·s;ν是光的频率。

②光能量

式中,c为真空中光速;R为里德伯常数,R=1.09677576×107m-1;m和n为整数;hν是光的一个单元的能量,是原子辐射前后的能差。

③对应的电子轨道半径

说明:ⓐ氢原子的电子只能在一定大小的、彼此分隔的一系列轨道上运动,原子具有一定的能量。ⓑ如果氢原子中的电子从一个大轨道上跳到小轨道上,原子的能量将从大变小,多余的能量释放出一个光子的能量。

④能够实现的电子轨道半径

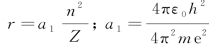
对氢原子,Z=1,可能的轨道是:r=a1,4a1,9a1,16a1,…最小轨道半径:a1=0.529177×10-10m。

式中常数:h=6.62620×10-34J·s;m=9.10956×10-31kg;e=1.60219×10-19C。

⑤氢原子的内部能量

式中,n=1,2,3,…,n称为量子数。这说明能量是分隔的,轨道是量子化的。

⑥里德伯常数

理论值:R=1.0973731×107m-1

实验值:RH=1.0967758×107m-1

⑦能级:与不同轨道对应的有不同分隔数量的能量。

⑧氢原子的电子轨道(如图6-4所示)

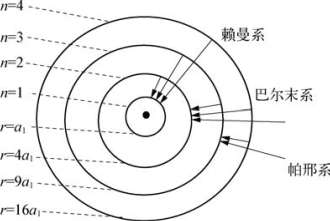
图6-4 氢原子的电子轨道

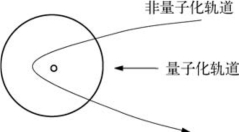
图6-5 电子跃迁

⑨氢原子的能级(略)

⑩电子跃迁:指电子从某一轨道跳到另一个轨道,如图6-5所示。

如果电子从非量子化轨道跃迁到量子化轨道,原子要发射一个光子,其能量是:

式中,h为普朗克常量。

6.类氢离子光谱

(1)类氢离子:原子核外只有一个电子,但是原子核带有大于一个单位的正电荷(氢原子Z=1),这些原子是离子。(www.xing528.com)

①一次电离的氦离子He+(Z=2)

式中,如n1=1,则n2=2,3,4,…

②二次电离的锂离子Li2+(Z=3)

式中,如n1=1,则n2=2,3,4,…

③三次电离的铍离子Be3+(Z=4)

式中,如n1=1,则n2=2,3,4,…

(2)里德伯常数的变化(在类氢离子中)

在类氢离子的光谱中发现那些与氢谱线重合的线稍有波长的差别,可能的原因是里德伯常数的不同。

①电子和原子核共同绕质心运动的折合质量:

式中,M为原子核质量;m为电子质量。

②里德伯常数的理论值和实验值:

式中,R∞为理论值,R∞=10973731m-1,相当于原子核质量无限大时的值;RA为实验值,因不同原子的M不同而变化。

7.椭圆轨道理论

(1)量子化通则

电子围绕原子核运动为圆形轨道时:

∮pdq=nh(n=1,2,3,…)

式中,dq是位移或角位移;p是与q对应的角动量;∮表示一个周期的积分。

(2)实际上,电子围绕原子核的运动轨迹是一个椭圆形轨道,圆形轨道仅是一个特例。

①椭圆形轨道

如图6-6所示,电子在椭圆运动中的位置可用极坐标表示。r和ϕ是两个坐标,对应的角动量和动量分别是pr和pϕ。

pϕ=mr2ϕ0 pr=mr0

式中,ϕ0是电子的角速度;r0是r方向的速度分量;rϕ0是垂直于r的速度分量。

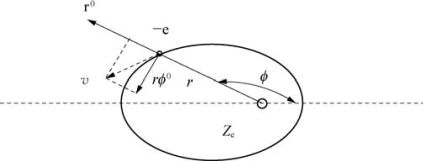
图6-6 椭圆形轨道

②对每一个坐标引入量子条件:

∮pϕdϕ=nϕh ∮prdr=nrh

式中,nϕ和nr都是整数;nϕ称角量子数;nr称径量子数。

③半长轴和半短轴

图6-7中,椭圆轨道半长轴:

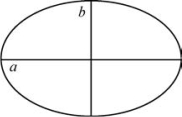
图6-7 半长轴和半短轴

椭圆轨道半短轴:

二者的关系:

式中,n=nϕ+nr,称主量子数;nϕ=1,2,3,…,n;nr=n-1,n-2,n-3,…,0。

④在椭圆轨道理论中,原子的能量与玻尔理论的描述完全相同:

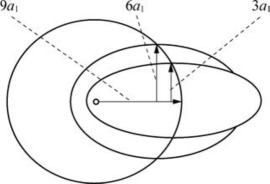
图6-8 椭圆轨道相对大小

⑤椭圆轨道相对大小

如图6-8所示,3a1:n=3,nϕ=1;6a1:n=3,nϕ=2;9a1:n=3,nϕ=3;

同一个n,有n个可能的轨道,即有n个运动状态,但它们的能量都是相同的,这种情况称n重简并。但是,在氢原子或类氢离子中,根据相对论原理,同一个n,有不同形状的轨道,每种轨道具有不同的能量。

8.在磁场或电场中的电子轨道

(1)史特恩-盖拉赫实验:显示原子在磁场中的取向量子化。

(2)电子轨道运动的磁矩

式中,nϕ=1,2,3,…;μB=0.92732×10-23A·m2,这是轨道磁矩的最小单元,称玻尔磁子。

9.玻尔理论的缺陷

(1)玻尔的量子规律与经典物理规律存在显著差异。

(2)玻尔的量子规律的特点显示了物理量的不连续性,例如原子内部的能量具有间隔的数字,能量的改变只能通过能级之间的跃迁。

(3)玻尔理论只能计算氢原子和类氢离子的光谱频率,这就需要更完整的理论——量子力学。

6.3.3 电子碰撞研究

1.夫兰克-赫兹实验

(1)用电子碰撞原子的方法,即用与发射光谱不同的方法研究原子的量子化能级。

(2)实验

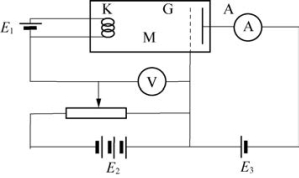
图6-9 夫兰克-赫兹实验

如图6-9所示,电子从热阴极K发出,在K与栅极G之间加上电场使电子加速,在G与接收极A之间有一个0.5V的反向电压。在玻璃容器M中充满汞气。

现象:①当K、G之间的电压从0逐渐增加,A极电流上升。

②当电压为4.1V时,电流突然下降,不久又上升。

③当电压为9.0V时,电流又突然下降,不久又上升。

④当电压为13.9V时,……

解释:①电子被加速后获得的能量是eV,e是电子电量,V是加速电压。一粒电子经1V电压加速后获得的能量为1电子伏特,即1.60×10-19J。

②当电压为4.9V(由于仪器上存在接触电势,实际读数为4.1V)时,称为汞的第一激发电势,电子获得4.9电子伏特的能量,如果该电子与汞原子碰撞,汞原子就从最低能级激发到较高能级;反之,如果汞原子从较高能级跃迁到最低能级,就释放出4.9电子伏特的能量,并且有光的发射:

hν=h/λ=eV

波长λ=250nm

结论:①原子被激发到不同的状态,吸收到不同的能量,这些数值是不连续的,可见原子内部的能量是量子化的,由此证明原子能级的存在。

②如果使电子在电场中加速,碰撞原子,刚好足以使原子中的电子离去(电离),这个电势差称为电离电势。