现代光学：光学谐振腔结构分析

5.9.1 结构图

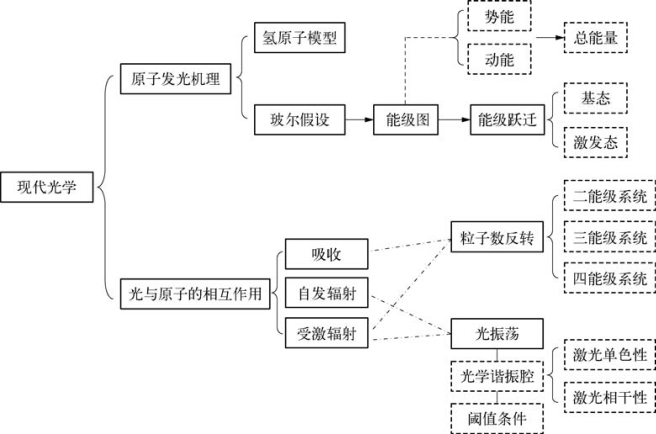
5.9.2 原子发光机理

1.氢原子模型

图5-68中,单个负电荷的电子e,质量为m,带正电荷的原子核Ze,质量为M。电子围绕原子核旋转。其向心力:

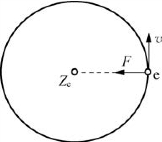
图5-68 氢原子模型

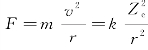
式中,r为电子和原子核之间的距离,即原子半径;v为电子绕原子核转动的速度;k为玻耳兹曼常数。

2.玻尔假设

(1)定态假设

原子只能处于一系列不连续的能量状态,这些状态称为定态。

(2)角动量量子化条件

式中,电子的角动量mvr只能是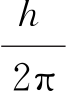的整数倍,即n=1,2,3,…;h为普朗克常量。即:电子运动的轨道不是任意的,只能是一些量子化的轨道。

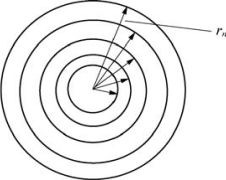
图5-69 电子运动轨道

图5-69中,n=1,2,3,…对应的电子轨道半径是r1,r2,r3,…,n愈大,r愈大,v愈小。

①电子的轨道半径:

②电子的轨道速度:

③能级图

ⓐ在每一个轨道时的电子势能:

ⓑ在每一个轨道时的电子动能:

ⓒ总能量:

En=Ep+Ek

式中,总能量是负的,表示要把电子从原子中移开必须对电子做功。

(3)频率条件

当原子从能量En的定态跃迁到能量Ek的定态时,就要发射或者吸收一个频率为νkn的光子:

①当En＞Ek时,发射光子;当En＜Ek时,吸收光子。

②能量最低的状态叫基态,能量较高的状态叫激发态。

5.9.3 光与原子的相互作用

1.人们对于光的各种了解,均通过光与物质的相互作用而获得,也就是光与原子的作用。

2.这种作用有三个主要过程:吸收、自发辐射和受激辐射。

(1)吸收

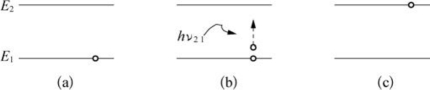
图5-70 吸收过程

如图5-70所示,处于基态E1的原子吸收了一个能量为hν的光子后,这个原子从基态E1激发到激发态E2。必须指出,只有光子的能量正好等于能级间隔(E2-E1)时,光子才能被吸收。

n12=n1ω12=n1B12u(ν)

式中,n12为在单位体积和单位时间从基态E1跃迁到激发态E2的原子数;n1为处于基态E1的原子密度;B12为吸收系数;B12u(ν)为吸收速率;u(ν)为光的辐射能量密度。

(2)自发辐射

如图5-71所示,处于激发态E2的原子放出一个能量为hν的光子后,这个原子从激发态E2回到基态E1。

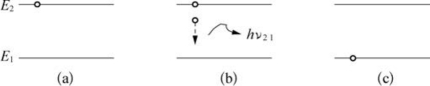
图5-71 自发辐射过程

n21=n2A21

式中,n21为在单位体积和单位时间从激发态E2到基态E1的原子数;n2为处于激发态E2的原子密度;A21为自发辐射系数。

图5-72 受激辐射过程

(3)受激辐射

如图5-72所示,处于激发态的原子,受外来光子的影响,从高能态向低能态跃迁,并把两个状态之间的能量差以辐射光子的形式辐射出去。

n'21=n2ω21=n2B21u(ν)

式中,n'21为在单位体积和单位时间内受激发射原子数;n2为处于激发态E2的原子密度;B21为受激辐射系数;B21u(ν)为辐射速率;u(ν)为光的辐射能量密度。

(4)三个过程的三个系数:B12、A21和B21

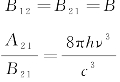(www.xing528.com)

3.粒子数反转:讨论受激辐射和吸收之间的关系

激光就是通过辐射的受激发射实现光的放大,即:一个光子hν射入一个原子体系后,在离开原子体系时,成为两个或更多个光子,而且这些光子的特征完全相同。

问题是:实际上,吸收、自发辐射和受激辐射是同时存在的,如何才能实现只有受激辐射存在呢?

当原子体系处于热平衡态时,吸收过程总胜过受激过程。如果破坏这种平衡态,必须使n2＞n1,这称为粒子数反转。如何实现粒子数反转?

①只有两个能级的物质不能实现。

②有三个能级的物质能够实现,例如:红宝石激光器。但是,这一过程需要相当强的外界抽运,这是它的一个显著缺点。

③有四个能级的物质比较容易实现,例如:YAG激光器。

4.光振荡:讨论受激辐射和自发辐射之间的关系

(1)光学谐振腔

在如图5-73所示的激光器中,能够实现粒子数反转的工作物质是放大元件。在光学谐振腔中,放大元件起着正反馈、谐振和输出的作用。

能实现粒子反转的工作物质受到外界作用后,许多粒子跃迁到激发态去,而这些激发态的粒子是不稳定的,它们在激发态的寿命时间内纷纷跳回到基态,发射出自发辐射光子。其中,偏离轴向的光子很快逸出谐振腔外,而沿轴向的光子在谐振腔内受到两端两块反射镜的反射作用,没有逸出腔外,引起轴向受激辐射,并且不断产生受激辐射,这种放大和振荡的过程使谐振腔内沿轴向的光骤然增加,这就是激光。

光学谐振腔可分以下几类。

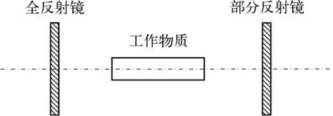
图5-73 光学谐振腔

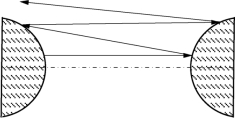
图5-74 不稳定谐振腔

①不稳定谐振腔

②稳定谐振腔

ⓐ平行平面腔

ⓑ同心谐振腔(略)

ⓒ共焦谐振腔(略)

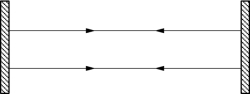
图5-75 平行平面腔

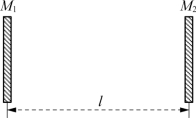
图5-76 阈值条件

(2)阈值条件

有了稳定的光学谐振腔,有了能够实现粒子反转的工作物质,还需要有其他条件。

图5-76中,M1和M2为两块反射镜。其阈值条件必须满足的条件为:

式中,α(ν)为工作物质的增益系数;l为两块反射镜间的距离;R1和R2分别为两块反射镜的反射率。

(3)激光的单色性

①原子的发光是有间隙的。

②原子发光的寿命(发光时间)Δt与发光的频率Δν是成反比的,即:Δt愈长,Δν宽度愈窄,光波的单色性愈好。

③只有那些满足谐振腔共振条件而又落在工作物质的谱线宽度内的频率才能形成激光输出,那些不满足共振条件的频率,都在谐振腔内干涉相消了。

④满足共振条件的频率:

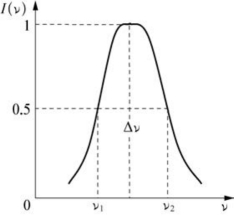
图5-77 谱线宽度

式中,j为整数;d为谐振腔长度。

⑤谱线宽度Δν为光谱线最大强度的一半所对应的两个频率之差(ν2-ν1)。

(4)激光的相干性

①相干性:空间内任意两点光振动之间的相互关联程度。

ⓐ完全相干光

图5-78中,P1和P2两个光振动在Q点相遇,两个光振动之间的位相差恒定,在Q点将得到稳定的干涉条纹。

ⓑ完全非相干光

图5-78中,如果两个光振动之间的位相差是完全任意的,并随时间作无规则变化,在Q点无法得到干涉条纹。

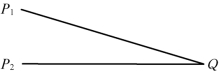
图5-78 完全相干光

ⓒ当P1和P2是两个重合的点,考虑它们不同时刻的光振动,我们称之为时间的相干性。

ⓓ当P1和P2是两个不同的点,考虑它们同时刻的光振动,我们称之为空间的相干性。

②普通光源的相干性

光的相干性很差。但是,利用单色分光仪得到的时间相干性可以很高。

③激光的相干性

ⓐ时间相干性(略)

ⓑ空间相干性(略)

④激光器的种类(略)