光的衍射现象及其在物理学中的重要性

5.5.1 结构图

5.5.2 光的衍射概述

光波通过小孔、小圆屏等障碍物时偏离原传播方向,进入其几何阴影区,并在屏幕上出现明暗相间的条纹,即光强不均匀分布。只有障碍物的线度和波长可以比拟时,衍射现象才能明显。

1.衍射分类

衍射系统由光源、衍射屏(衍射孔或障碍物)和接收屏组成。按照它们之间的相互位置,可以分为两类。

(1)菲涅耳衍射:衍射屏与光源或与接受屏之间的距离都是有限的,也称近场衍射。

(2)夫琅禾费衍射:衍射屏与光源或与接受屏之间的距离都是无限的,也称远场衍射。

2.惠更斯原理

任何时刻波面上的每一点都可以作为次波的波源,各自发出球面次波。在以后的时刻,所有这些次波波面的包络面形成整个波在该时刻的新的波面。波面是指光波在传播时同位相各点的轨迹。

如图5-42所示,SS'为t=0时刻的波面,箭头表示光的传播方向;MM'为下一时刻的波面。

图5-42 波面

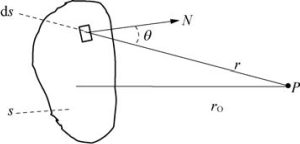
图5-43 惠更斯-菲涅耳原理

3.惠更斯-菲涅耳原理

惠更斯-菲涅耳原理是对惠更斯原理的改进。

如图5-43所示,波面s上的每一个面积元ds都可以看成是一个新波源,它们都发出次波;N为ds的法线;P为ds到达的一点;r为ds到P的连线;θ为N和P的夹角。

(1)次波在P点的位相:

式中,n为透明介质的折射率。

图5-44 菲涅耳半波带

(2)次波ds在P点的合振动:

式中,K(θ)为与θ增减有关的函数;C为比例系数。

(3)整个波面s在P点的合振动:

(4)应用:菲涅耳半波带

如图5-44所示,O为点光源,SS'为通过圆孔时的波面,R为波面半径,PO为光达到圆孔面对称轴上的一点,rO为PO与波面极点BO之间的距离,r1为PO与波面极点B1之间的距离,r2为PO与波面极点B2之间的距离。

设想:将波面分成许多环形带,相邻带的边缘到PO点的距离相差半波长:

相邻两带的对应部分所发出的次波到达PO点的光程差为λ/2,即它们以相反的位相同时到达PO。这样分成的环形带称为菲涅耳半波带。

光传播到任一观察点P时的合振幅:

式中,a1为第一个半波带的振幅;ak为最末一个半波带的振幅,k为奇数取“+”,k为偶数取“-”。振幅大小就是光的强弱。

5.5.3 菲涅耳衍射

1.圆孔衍射

如图5-45所示,O为点光源,ρ为光阑BB'上的圆孔半径,SS'为通过圆孔时的波面,PO为光达到圆孔面对称轴上的一点,rO为PO与波面极点BO之间的距离,h为ρ与BO之间的距离。

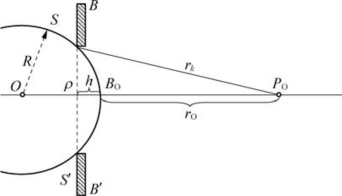
图5-45 圆孔衍射

(1)PO点合振幅的大小取决于露出的带数k的多少。

(2)与k为奇数相对应的那些PO点,合振幅Ak较大;与k为偶数相对应的那些PO点,合振幅Ak较小。

(3)当k=1时,合振幅:

A=a1

(4)当圆孔半径ρ无限大时,合振幅:

式中,a1为第一个半波带的振幅。

2.圆屏衍射

图5-46 圆屏衍射

如图5-46所示,O为点光源,B为不透明小圆屏,PO为所有次波到达的一点。小圆屏B遮蔽了开始的k个波带,k+1次波能够到达PO点。无论小圆屏B的大小和位置如何,在它的几何投影中心永远有光,而小圆屏B愈小,到达PO点的光愈强。(www.xing528.com)

(1)菲涅耳波带片是根据圆屏衍射原理制造出的光学元件。

(2)衍射现象是光的波动性的最基本表现,光的直线传播是衍射现象的极限表现。

5.5.4 夫琅禾费衍射

1.单缝衍射

如图5-47所示,平行光线M穿过狭缝BB',缝宽为b,各次波透过凸透镜L,在焦平面FF'上会聚于P点,出现明暗条纹。

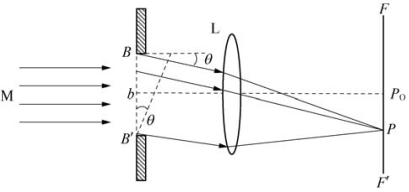
图5-47 夫琅禾费衍射

(1)P点光强

式中,u=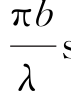sinθ;I为中心明纹处P点光强。OO

(2)衍射花纹

当bsinθ=±2k,k=1,2,3…时,中心为暗条纹;

当bsinθ=±(2k+1),k=1,2,3…时,中心为明条纹。

①中央最大值的光强最强。

②亮条纹到凸透镜中心所张的角度称角宽度,中央亮条纹的角宽度等于2λ/b,即为其他亮条纹角宽度的2倍。

③任何两个相邻暗纹之间为一个亮纹,两侧亮纹的角宽度为:

Δθ=λ/b

2.圆孔衍射

(1)大多数光学仪器中使用的透镜的边缘(即光阑)都是圆形的,而大多数又都是通过平行光或近似平行光成像。因此,夫琅禾费用圆孔衍射代替单缝衍射具有重要意义。

(2)图5-48中,L1和L2为两块凸透镜,在A屏上有一半径为r的小圆孔。光线通过L2后,在焦平面上(B屏)可以得到圆形的衍射花纹。

①屏B上任一点的光强计算(略)。

图5-48 圆孔衍射

②爱里斑:B屏中央是一个较亮的圆斑,外围是一组同心的暗环和亮环,这个中央亮斑集中了83%的衍射光能量,也就是几何光学像点。

图5-49 爱里斑能量示意图

③爱里斑的半角宽度:

θ1≈sinθ1=0.61λ/r

④爱里斑的半径:

式中,f为L2凸透镜的焦距;D为圆孔直径。

3.光栅衍射

光栅是由大量等宽和等间距的平行狭缝构成的光学元件。

①如图5-50所示,平行光线M垂直入射穿过BB'四条狭缝时,缝宽均为a,相邻不透光部分宽均为b,d=a+b称为光栅常数。

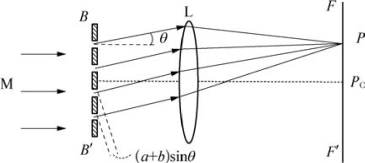
图5-50 光栅

各次波透过凸透镜L,在FF'暗屏上出现一系列分得很开的又细又亮的条纹,称为光栅光谱。

光栅方程决定明纹的位置:

(a+b)sinθ=±kλ (k=0,1,2,…)

②平行光线M倾斜入射穿过BB'四条狭缝时,入射角为φ。

光栅方程决定明纹的位置:

(a+b)(sinθ±sinφ)=±kλ (k=0,1,2,…)

缺级:当a和b存在某种关系时,光栅中某些明条纹不出现。

4.布拉格方程

X射线在晶体表面掠射时,表达衍射线相干的情况。

5.光学仪器的分辨能力

(1)像的分辨能力。

(2)色的分辨能力。

小结:①光的干涉和光的衍射都是波的相干叠加后产生的结果。

②光的干涉和光的衍射都出现明暗相间的条纹或圆环。

③光的干涉是有限数量波的相干作用,光的衍射是无穷多次波的相干作用。