普通物理学知识结构分析：几何光学

5.2.1 结构图

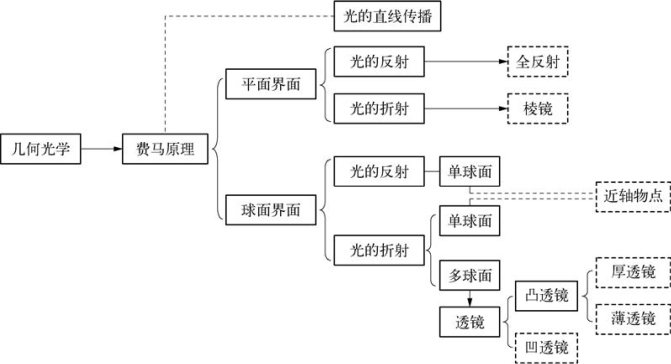
5.2.2 费马原理

1.光线:形象地表示光的传播方向的几何线。

2.费马原理:当两列波在同一点相遇而叠加时,其光强取决于位相差,而位相差又取决于光程差。

(1)费马指出:光在指定的两点之间传播,实际的光沿光程值最小、最大或恒定的路程传播。

(2)数学表达式:

式中,nds=cdt为光程;n为折射率;s为两点之间的距离;c为真空中的光速。

由此,直接引入光的直线传播定律,以及光的反射定律和光的折射定律。

3.几何光学的基本实验规律

(1)光的直线传播定律:在均匀介质中,光沿直线传播。

(2)光的独立传播定律:不同方向或不同物体发出的光线相交,对每一条光线独立传播不产生影响。

(3)光的反射定律:光线传播到两种介质表面时,一部分光线改变方向返回原来的介质传播。

(4)光的折射定律:光线传播到两种介质表面时,一部分光线改变方向进入另一种介质传播。

4.几个概念

(1)单心光束:把发光点看成是一个发散光束的顶点。

(2)物:来自实物的光线直接进入人的眼睛。

(3)实像:发散光束中的各条光线实际在该点会聚成的一个顶点。

(4)虚像:在发散光束的反向延长线寻找到光束会聚的一个顶点。

5.2.3 光在平面界面上

1.光的反射

图5-1中:发光点P发出的a光线和b光线到达平面镜NN'后,根据反射定律,光线的反向延长线会聚于P0点,这就是发光点P的虚像,即光束顶点P的虚像,而且P0与P是对称于平面镜的。单心光束没有破坏。入射角i1等于反射角i2。

图5-1 光的反射

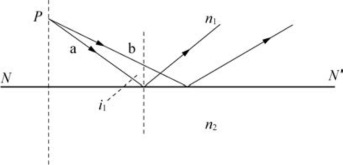
图5-2 全反射

2.全反射

(1)光线没有折射,全部被界面反射回原介质。最大入射角ic称临界角。如图5-2所示。

(2)光纤维就是根据全反射原理制造的。

3.光的折射

图5-3中,发光点P发出的a光线和b光线到达折射率不同的两种透明介质的分界面NN'后(折射率分别为n1和n2),根据折射定律,光线改变方向,但反向延长线会聚于P0点。

sini1/sini2=n2/n1

n1=c/v1 n2=c/v2

式中,c为光在真空中的速度;v1和v2分别为光在两种介质中的速度。

图5-3 光的折射

图5-4 棱镜

4.棱镜

图5-4中,A为折射棱角。入射光线连续两次折射后,出射线与入射线的交角又称偏向角:

∠BEC=θ=i1+i2-A

当i1=i2时,

θ0=2i1-A

棱镜材料折射率:

5.2.4 光在球面界面上

1.反射(单球面)

图5-5 单球面上的反射

图5-5中,C是凹球面的球心,也称曲率中心;AOB是凹球面的一部分,凹球面的中心点O称顶点;r是凹球面半径,也称曲率半径;CO称主轴;P为发光点;PA为任意的一条入射光线;AP0为反射光线;P1为反射光线AP0与主轴CO的交点。

式中,像距s1的“-”表示数值在顶点O的左方,“+”表示在右方。

说明:当发光点P到顶点O的距离固定时,就可以计算出任意一条反射光线与主轴CO的交点P1的位置(即-s1的大小)。但当-u的大小变化时,P1的位置也将变化,即:发光点的单心光束经球面反射后,将不再保持单心。

如图5-6所示,如果有两条入射光线A1和A2,它们分别与主轴CO相交于P1和P2(图中圆环处),而两根反射光线本身又相交于P3,P3不在主轴CO上。由此又引入子午像线和弧矢像线。

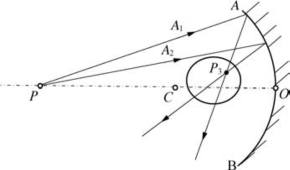
图5-6

图5-7

如图5-7所示,如果考虑近轴光线(单心光束没有被破坏),即(-u)和(-u1)都足够小时,就会有明确的像点在主轴CO上出现。

球面反射物像公式:

式中,s1为反射光线在主轴CO上所成的像P1到顶点O的距离(OP1),称像距;s为发光点P到顶点O的距离(OP),称物距;f称焦距,即平行光束M经凹球面反射后在主轴CO上会聚的一点到顶点O的距离。

2.折射(单球面)

图5-8中,球面AA0的左面介质的折射率为n,右面介质的折射率为n0,发光点P在球面AA0的左面,PA为入射光线,AP0为折射光线。得到:

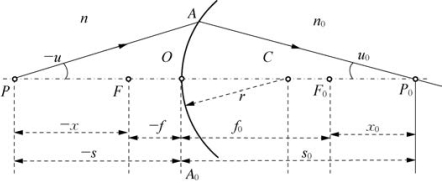
图5-8 单球面上的折射

式中,像距s0即P0点所在的位置,与u的大小有关,说明从发光点P发散的单心光束经过折射后,单心性被破坏。

如果考虑近轴光线(单心光束没有被破坏),即(-u)和(-u0)都足够小时,就会有明确的像点出现在主轴CO上。

球面折射物像公式:(www.xing528.com)

如果把发光点P和像点P0互换,物像公式依然成立,这种关系称为共轭。说明光路是可逆的。

(1)高斯公式

式中,f为物方焦距,在主轴CO上的一个物点,其发出的光经折射后产生平行于光轴的平行光束,该点称为物方焦点F,该点到球面顶点O的距离称为物方焦距。f0为像方焦距,平行于主轴CO的入射光线经折射后与主轴相交的点称为像方焦点F0,该点到球面顶点O的距离称为像方焦距。

(2)牛顿公式

xx0=ff0

3.折射(多球面)

图5-9中,1和4为凸面镜,2和3为凹面镜。发光点P经过1、2、3和4面镜时,分别单独成像,最后成像在P0。

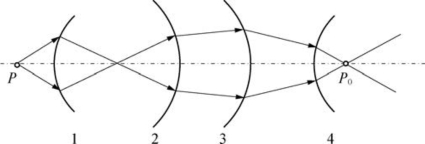
图5-9 多球面上的折射

(1)凹球面折射

图5-10中,P为实物,P0为虚像。

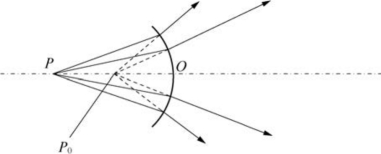
图5-10 凹球面折射

(2)凸球面折射

图5-11中:P1为实像,P0为虚像。

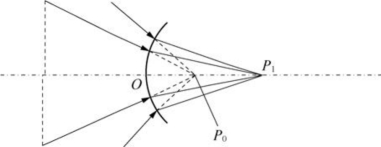
图5-11 凸球面折射

(3)实物和虚物

①实物:由发散的入射光束的顶点(不管是否有实际光线通过这个顶点)所形成。

②虚物:由会聚的入射光束的顶点(永远没有实际光线通过这个顶点)所形成。

4.透镜

(1)凸透镜(中间比边缘厚,如图5-12所示)

图5-12 凸透镜

①厚透镜(透镜厚t不能忽略)

图5-13中,n为厚透镜折射率,n1为物方折射率(透镜左方),P为物点,(-s)为物距,n2为像方折射率(透镜右方),P1为像点,(s1)为像距,t为厚透镜厚度,(-r2)为右球面曲率半径,(r1)为左球面曲率半径。

图5-13 厚透镜

先考虑P发出的光线经凸球面AOB后折射,在P1处成实像,像距为s1。凸球面AOB物像公式:

再考虑光线经凸球面AO1B后折射,在P2处成虚像,像距为s2。凸球面AO1B物像公式:

②薄透镜(透镜厚t可以忽略)

物像公式:

简化成普遍的高斯公式:

式中,f为物方焦距,f1为像方焦距。

简化成普遍的牛顿公式:

xx1=ff1

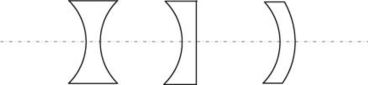
图5-14 凹透镜

(2)凹透镜(中间比边缘薄,如图5-14所示)

小结:①以上讨论的都是点光源发出的光线,而且是在近轴条件下的成像。实际上,点光源是不存在的;

②任何物体上的每一点都可以看成是一个发光点。

5.近轴物点

(1)近轴物在近轴光线条件下凹球面反射的物像公式

图5-15中,O为凹球面顶点,直线QP垂直于主轴OO1,成像直线Q1P1也垂直于主轴OO1,A为入射点,O1P为物距(-S),O1P1为像距(-S1)。

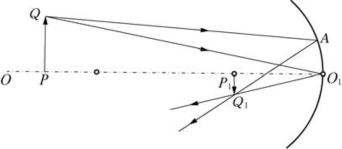
图5-15

物像公式:

式中,r为焦距;y为PQ(物高);y1为P1Q1(像高)。

因此,不在主轴上的发光点Q能够成像于单独一个像点Q1,必须满足的条件是:①光线必须近轴;②物点必须近轴。

(2)近轴物体在近轴光线条件下凸球面折射的物像公式

图5-16中,凸透球面AA'的左面介质的折射率为n,右面介质的折射率为n1,发光物PQ在球面AA'的左面,垂直于主轴,所成的像P1Q1也垂直于主轴。

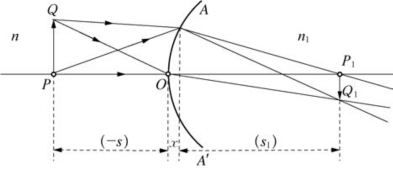
图5-16

物像公式:

式中:y=PQ,y1=P1Q1

6.多球面光学系统简述

(1)重要概念:

①焦点和焦平面;

②主点和主平面;

③节点。

(2)作图求像法(见前述)

(3)物像公式(见前述)