交流电路的解法：矢量图解法

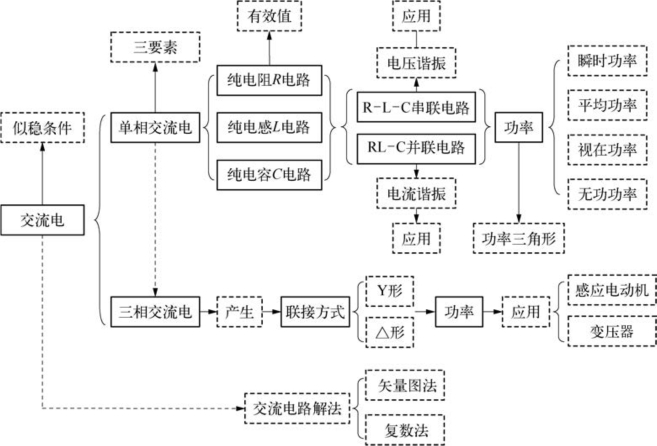
4.9.1 结构图(见下页图)

交流电是指电流的大小和方向都随时间作周期性变化的电流。但是,在一定的条件下可以看成似稳电流:

r≪cT

式中,r为电流系统中相隔最远的两点的距离;c≈3×108m/s;T为电流变化的周期。

本节只讨论似稳电流。

交流电在电能的产生、传送和利用等方面比直流电有着许多不可比拟的优点。

4.9.2 单相交流电

图4-41显示的是一个线圈在磁场中转动时产生的正弦(或余弦)式交变电压。

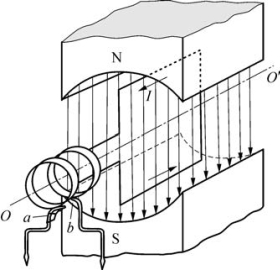
图4-41 交变电压的产生

u=Umsin(ωt+φ)

式中,u为电压的瞬时值;Um为幅值;ω为角频率(或圆频率);(ωt+φ)为位相;φ为初位相;f=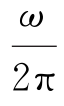为交流电频率。

交流电量瞬时值的三要素:振幅、频率、位相。

1.纯电阻R电路

一交变电压加在电阻R两端,电路中的电流强度:

式中,电流幅值为Im=Um/R。电流与电压频率相同,位相相同。

有效值I:一个交流电通过一个电阻时,在一个周期内产生的热量与一个稳定电流通过该电阻时产生的热量相等。那么,这个稳定电流的量值就是交流电电流的有效值。

对于正弦(或余弦)式电流:

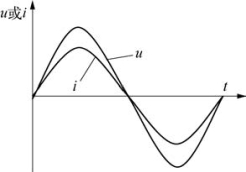
图4-42

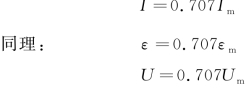
式中,I为电流有效值;Im为电流幅值;ε为电动势有效值;εm为电动势幅值;U为电压有效值;Um为电压幅值。

说明:各种交流电电器设备的额定电压和额定电流分别是指各自的有效值。

2.纯电感电路

一交变电压加在电感L两端,电路中的电流强度:

式中,电流幅值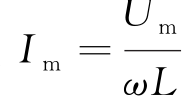。电流与电压频率相同,但位相落后π/2。引入感抗:X= L ωL。

应用:扼流圈用来控制交流电路中的电流。

3.纯电容电路

一交变电压加在电容C两端,电路中的电流强度:式中,电流幅值Im=ωCUm。电流与电压频率相同,但位相超前π/2。引入容抗:XC=。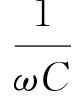

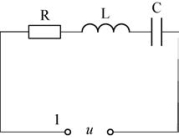
图4-43 R -L -C串联电路

4.混合电路

(1)R -L -C串联电路

电路中的电流:

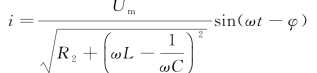
式中,u=Umsinωt为交变电压。

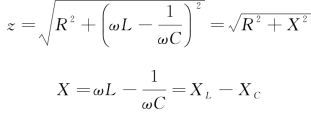
式中,z为阻抗,X为电抗,XL为感抗,XC为容抗。

电路中的电流幅值和电压幅值:

两边同时除以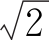得到电路中的电流有效值和电压有效值:

电流和电压的相位差:

电阻、电感和电容两端的电压:

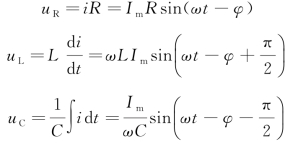
式中,电阻上的电压与电流同位相,电感上的电压位相超前电流π/2,电容上的电压位相落后电流π/2。

讨论:

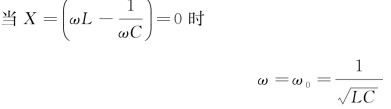
式中,ω为角频率或圆频率;ω0为串联谐振频率。

电路发生电磁谐振(共振),称为串联谐振或电压谐振。此时,电容或电感上的电压是总电压的Q倍:

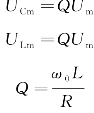
式中,Q为品质因数,简称Q值。

应用:调谐器。

(2)RL -C并联电路

讨论:

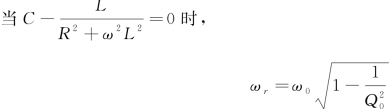(www.xing528.com)

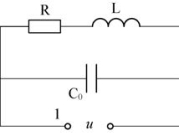
图4-44 RL- C并联电路

式中,ωr为并联谐振频率。

电路发生电磁谐振(共振),称为并联谐振或电流谐振。此时,电容支路或电感支路上的电流有效值是总电流的Q0倍:

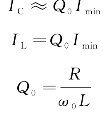
应用:中频放大器。

5.功率

(1)瞬时功率

p=iu=Umsinωt·Imsin(ωt-φ)

式中,u为电源电压;i为电路电流。

(2)平均功率(有功功率)

P=UIcosφ

式中,U为电压有效值;I为电流有效值;cosφ为功率因数。

典型情况有如下几种。

①纯电阻:P=UI=I2R;

②纯电感:P=0;

③纯电容:P=0;

④一般情况:。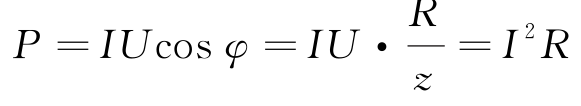

(3)视在功率

S=UI并不代表电路中消耗的实际功率,仅表示电机或变压器的容量。

(4)无功功率

Q=IUsinφ

式中,φ为有效电流和有效电压的相位差。

(5)功率三角形分析

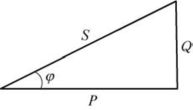
图4-45 功率三角形

cosφ与电路元件有关,例如在日光灯中。

4.9.3 三相交流电

1.产生

三个完全相同的绕组,频率相同,位相差120°,如图4-46所示。

三个电动势:

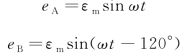
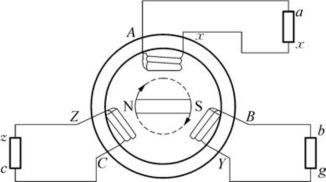
图4-46 三相交流电

eC=εmsin(ωt-240°)

每个绕组两端的电压称为相电压,全部采用Uφ表示。

2.联结方式

(1)电源连接:①星形接法(或Y形接法);②三角形接法(或△形接法)。

(2)负载连接:①星形接法;②三角形接法。

3.功率

(1)三相交流电由三个单相交流电组成,所以三相功率是三个单相功率之和。

(2)平均功率

①P=3UφIφcosφ

式中,Uφ为相电压;Iφ为相电流;φ为电流和电压的位相差。

②P=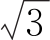UiIicosφ

式中,Ui为线电压;Ii为线电流;φ为电流和电压的位相差。

说明:电流和电压均为有效值,且无论负载是何种连接。

(3)应用

①感应电动机:利用旋转磁场把电能转换成机械能;

②变压器:利用互感现象改变交变电压的高低。

4.9.4 交流电路的解法

1.矢量图解法

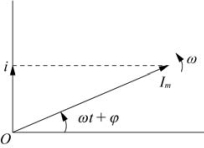
图4-47 矢量图解法

图4-47中,有一个随时间变化的交变电流(或电压)i=Imsin(ωt+φ),与一个旋转矢量相对应。Im为交流电幅值,ω为交流电角速度,沿逆时针旋转,(ωt+φ)为交流电位相,Im在纵坐标上的投影i就是交流电的瞬时值。

如果有两个同频率的交流电叠加,可以用矢量图法解决电路问题。

2.复数解法

解决矢量图法不能解决的问题(具体解法略)。