电介质在静电场中的性质

4.4.1 结构图

4.4.2 电介质

1.电介质:在一般条件下,是指导电性能极差的物质,例如玻璃。

2.电介质极化:在平行板电容中插入电介质后,如图4-11所示,平行板电容增大,为此引入电介质的极化概念,并进行一系列研究。

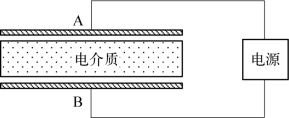
图4-11 电介质极化

式中,C为增大的电容;C0为原来的电容;εr为相对介电常数。

(1)电介质击穿:在很强的电场中,电介质的性能被改变后成为导体。

(2)达到击穿时的最大的电场强度称为电介质的绝缘强度,也叫介电强度。

3.电介质极化分类

(1)电介质的两类分子

电介质的每个分子由带负电的电子和带正电的原子核组成,我们把分子的全部电子看成有一个“重心”,我们把分子的全部原子核也看成有一个“重心”。(请注意:我们现在没有涉及原子)

①无极分子:如果在没有外电场的作用下,每个分子的两个“重心”重合,这类分子称无极分子。

②有极分子:如果在没有外电场的作用下,每个分子的两个“重心”不重合,这类分子称有极分子,相当于一个电偶极子。

(2)电介质的两类分子极化

①无极分子电极化

位移极化:无极分子在外电场的作用下,两个“重心”产生相对位移,位移的大小与电场强度成正比,这个过程叫位移极化。发生位移的主要是质量比原子核小得多的电子,所以也称电子位移极化,此时的每个分子成为一个电偶极子。当外电场消失后,分子又呈现电中性状态,如图4-12所示。

图4-12 位移极化

②有极分子极化

取向极化:即使没有外电场,每个分子也相当于一个电偶极子。当有外电场而且外电场增强时,分子电矩排列更整齐,这个过程叫取向极化。同时也发生位移极化。当外电场消失后,分子又呈现电中性状态,如图4-13所示。

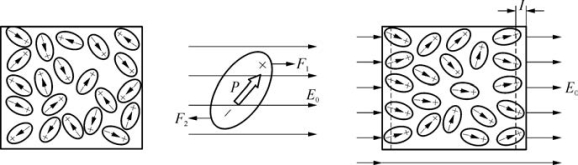
图4-13 取向极化

4.电极化强度:从宏观角度表示介质的极化程度的基本物理量。

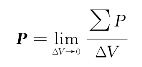
式中,P为电极化强度(又称极化矢量);ΔV为任取的体积元;P为分子电矩。P也就是单位体积的分子电矩矢量和。

(1)电极化强度与极化电荷

σ'=Pcosθ=P·en

式中,σ'为极化电荷面密度;P为电极化强度;en为表面外法线方向上的矢量;θ为P和en之间的夹角。(www.xing528.com)

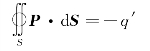
式中,P为电极化强度,dS为任意闭合曲面,q'为闭合曲面内的极化电荷总量。

(2)电极化强度与总电场强度

各向同性电介质:

P=ε0χE

式中,电极化矢量P与总电场强度E成正比,而且方向相同;ε0为真空介电常数;如果介质均匀,χ为比例系数,是一个恒量。

说明:①总电场强度E=E0(外电场强度)+E'(极化电荷产生的附加电场的电场强度)。

②电介质的极化改变了原来的外电场。

例如:平行板电容(图4-14)

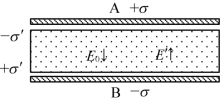
图4-14 平行板电容

式中,+σ和-σ为电容器极板上的电荷面密度;+σ'和-σ'为电介质极化电荷面密度;ε0为真空介电常数;εr为相对介电常数。

各向异性电介质:

式中,电极化强度P与总电场强度E方向不同;如果介质不均匀,χ要用9个量(张量)表示。

4.4.3 高斯定理

1.在真空的静电场中:

2.在电介质的静电场中:

图4-15 E0线

引入电位移矢量D,以消除∑q',得到:

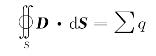
式中:D=ε0E+P,D·dS为通过dS面积的电位移通量。

3.外电场强度E0、放入电介质后总电场强度E和D的关系

说明:在E线图(图4-16)中,总电场强度E包括外电场强度E0(图415)和电介质电场强度E',而在D线图(图4-16)中已经没有E'。在真空中,当均匀介质充满外电场时,D=ε0E0。

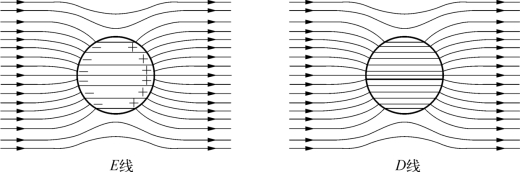
图4-16