分子运动论的基本原理

3.3.1 结构图

3.3.2 分子运动论

本节用分子运动论(微观结构)来解释理想气体的压强和温度,而压强(力学参量)和温度(热学参量)都是理想气体的状态参量,或者说,这部分内容是对状态参量的进一步探讨。

分子运动论是指:①一切宏观物体都由大量分子或原子组成。②分子在运动(布朗运动),这种运动,是永不停息的、无序的、与温度有关的热运动。③分子之间有相互作用力。

3.3.3 理想气体的微观模型

1.分子本身的线度与分子之间的平均距离相比,可以忽略不计。

2.在一般情况下,分子之间及分子与容器器壁之间没有相互作用。

3.如果有碰撞作用,也完全是弹性的,即分子动能没有损失。

3.3.4 理想气体的压强

1.实际上,大量的分子运动对容器器壁会产生持续的压力。2.压强:表示单位时间内单位面积器壁获得的平均冲量。

式中,n为分子数;ε-=1/2(m/v2),为分子平动动能的平均值。

说明:上式将宏观量p与微观量ε-联系起来。微观量ε-不能直接测定,但是宏观量p可以测定。

3.范德瓦耳斯方程

(1)理想气体是一个近似的模型,忽略了分子体积和分子间引力。

(2)对分子体积的修正:

式中,R为普适气体常数;T为气体温度;v为容器容积;b为气体分子所占体积的改正量,b≈10-5m3。

(3)对分子引力的修正:

式中,Δp=α/v2,为气体内压强;α为比例系数。

(4)方程(适用于1mol气体):

4.推证

(1)推证阿伏伽德罗定律。

(2)推证道尔顿分压定律。

3.3.5 理想气体的温度

式中,k为玻尔兹曼常数。

说明:宏观温度T是大量分子平均平动动能的量度。

3.3.6 理想气体的内能(www.xing528.com)

1.确定一个物体的空间位置,必须有独立的坐标数目,这个坐标数目称为物体的自由度。

2.分子和分子中的原子都存在自由度,包括平动自由度、转动自由度和振动自由度。

3.理想气体的平均平动能

4.能量按自由度均分定理

理想气体分子的每个自由度都具有相同的平均动能: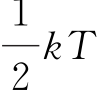

5.理想气体分子的平均总动能

式中,t为平动自由度;r为转动自由度;s为振动自由度。

6.理想气体的内能

(1)质量为M的理想气体的内能

式中,M为理想气体质量;μ为理想气体摩尔质量;t为平动自由度;r为转动自由度;s为振动自由度;k为玻尔兹曼常数;T为气体温度。

(2)1mol理想气体内能

3.3.7 理想气体的热容量

理想气体的热容量与分子的自由度有关。

1.物体热容量:温度升高(或降低)1℃时物质吸收(或放出)的热量。

式中,M为物质的质量;c为物质的比热。

2.摩尔热容量:1mol物质温度升高(或降低)1℃时物质吸收(或放出)的热量。

C=μc

式中,μ为物质的摩尔质量;c为物质的比热。

3.定容摩尔热容量:1mol的理想气体,在体积不变的条件下吸收热量dQ,温度升高dt。

说明,热容量只与分子自由度有关,与气体温度无关。对单原子分子气体:(t+r+2s)=3;对双原子分子气体:(t+r+2s)=7。

4.定压摩尔热容量

5.对热容量的影响

(1)振动动能的影响。

(2)转动动能的影响。