2.6.1 结构图
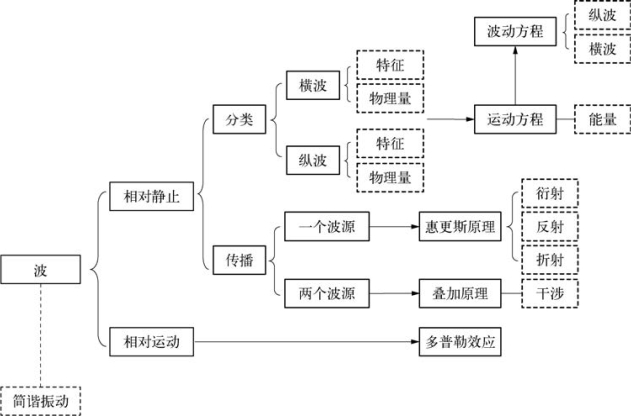
2.6.2 知识要点
1.基本概念
波是振动的传播。振动是一种运动状态,波也是一种运动状态。我们在前面讨论的振动,是机械振动中最简单的简谐振动。因此,我们现在讨论的波就是最简单的简谐振动形成的简谐波,而且是平面简谐波。即在简谐波的传播过程中,某一时刻振动相位相同的各点所形成的面的形状是平面的。此外,还有球面波等。除了机械波之外,波还包括电磁波。
小结:
机械振动—简谐振动

2.波源与介质
能够做机械振动的物体被称为波源。当物体振动以后,带动物体相邻的介质一起振动,依次传递,在相邻介质的传递中形成机械波。所以,形成波的两个必要条件是波源和介质。能够在振动以后恢复到原来平衡位置的介质被称为弹性介质。相对静止,是指振动波源与传播介质是相对静止的,观察者相对于传播介质也是静止的。这类问题比较简单。
相对运动,是指振动波源与传播介质是相对运动的,观察者相对于传播介质也是相对运动的。这类问题比较复杂。
3.波的分类
根据振动方向与传播方向的关系,可分为横波和纵波,如图2-47所示。
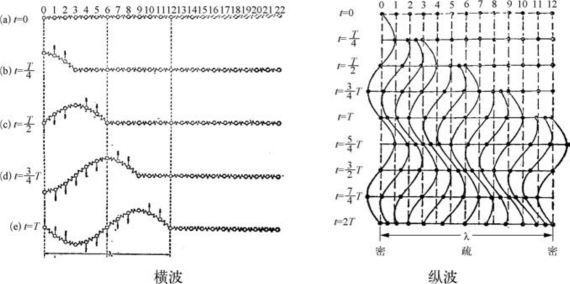
图2-47 横波和纵波
(1)介质的每个质元的振动方向与波的传播方向垂直的波称为横波。
(2)介质的每个质元的振动方向与波的传播方向相同的波称为纵波。
横波只能产生在固体中,纵波只能产生在流体中。
原因是,在固体中,一层介质相对于另一层介质平移而发生切变时,固体中会产生恢复这一切变的弹性力,使介质元在平衡位置附近振动起来,而流体中不能产生这种切变弹性力。其特征是:横波形成波峰和波谷,纵波形成密区和疏区。
4.相关物理量
(1)波长λ:相邻的两个振动位相相同的点之间的距离。
在横波中,就是两个相邻的同时达到波峰或波谷之间的距离。在纵波中,就是两个相邻的同时达到密区和疏区之间的距离。
(2)周期T:传播一个波长的距离所需要的时间,也是振动的周期。
(3)频率ν:在单位时间内,波的传播包含的完整波长的数目,也是振动的频率。
(4)波速v:在单位时间内,振动状态传播的距离。
![]()
5.简谐波的运动方程
简谐波的运动方程是定量描述位移与时间之间的关系,如图2-48所示。
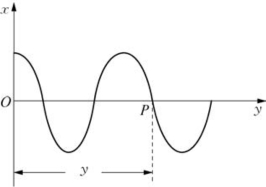
图2-48

式中,x表示沿Oy方向上各点的位移,常用形式有以下几种。
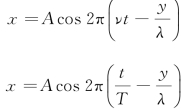
单独一点振动的初位相:
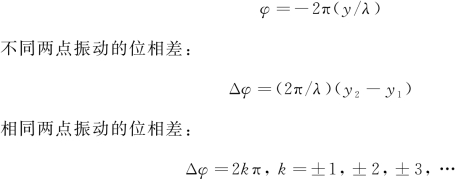
6.简谐波的波动方程
简谐波的波动方程是定量描述波速与传播介质的性质之间的关系。
(1)横波:
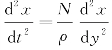
式中,N为介质的切变模量;ρ为介质的密度。
![]()
(2)纵波:
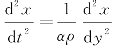
式中,α为介质的弹性系数。(https://www.xing528.com)

式中,Y为杨氏模量;α=1/Y。
7.能量
波是能量的传播过程。
在纵波中,
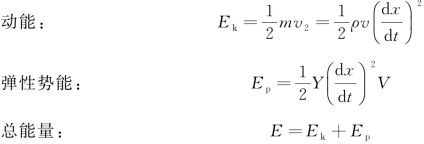
(1)能量密度描述单位体积中的能量:
![]()
能量密度在一个周期内的平均值:
![]()
式中,ρ为介质密度,A为振幅,ω为频率。
(2)能流密度描述单位时间内通过单位截面积的能量:
![]()

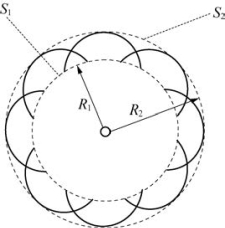
图2-49 一个波源
8.波的传播
(1)一个波源
惠更斯原理:波所达到的每一个点都可看作一个新的波源,然后从这些新的波源发出次波,而新的波前就是这些次波的包迹。
如图2-49所示,波从波源O以速度v向四周传播。时刻t的波前是半径为R1的球面S1。在下一时刻t+Δt,S1上的各点都可看作新的波源,半径为R1+vΔt,这些次波的包迹为球面S2。
用惠更斯原理可以做出如下解释。
①光的衍射:波可以绕过障碍物继续传播,但是传播方向发生改变。
②光的反射:波从一种介质传播到另一种介质时,一部分波从分界处返回原来的介质,遵守反射定律。
③光的折射:波从一种介质传播到另一种介质时,一部分波从分界处进入另一种介质,遵守折射定律。
(2)两个波源
①叠加原理:从几个波源产生的波在同一介质中传播时,在相遇处各质点的位移是各波单独存在时在该点位移的矢量和。
②波的干涉:如果两波源频率相同、振动方向相同、位相相同或有固定位相差时,在重叠处产生的简谐振动具有相同的频率、相同的振动方向、固定的位相差。但是,在重叠处会出现振幅大大增强或者完全抵消的现象。
③特殊的干涉现象:驻波。即两个振幅相同、频率相同、振动方向相同或相反传播(一个向y正方向,一个向y负方向)的波的叠加。驻波没有传播方向,也不传播能量。
④为了与驻波有所区别,一般其他的波被称为行波。
9.相对运动
从更大范围来说,如果波源和(或)观察者相对于传播介质运动时,我们会观察到一种新的现象,称为多普勒效应,现分成四种情况进行讨论,如图250所示。
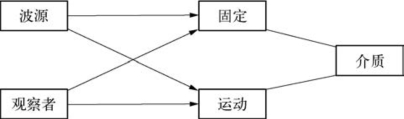
图2-50
(1)波源固定,观察者相对于介质静止(u=0,v=0)。
ν'=ν
即:观察者接收到的频率ν'等于波源的频率ν。
(2)波源固定,观察者以速度v相对于介质运动(u=0,v≠0)。
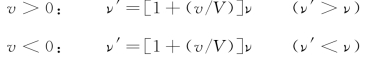
式中,V为波速。
(3)波源以速度u相对于介质运动,观察者静止(u≠0,v=0)。
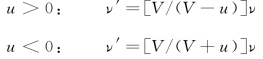
(4)波源与观察者同时相对于介质运动。 (u≠0,v≠0)
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




