普通物理学-振动共振-知识结构分析

2.5.1 概述

1.结构图

2.基本概念

振动是指物体在一定位置附近做来回重复的运动。振动是一种十分普遍的运动,例如:拉琴、敲鼓、打雷、地震。

简谐振动是振动中最简单、最基本的运动,例如:钟摆。

我们首先研究简谐振动,而且主要研究简谐振动。为什么?因为任何复杂的振动,都可以看作是两个或两个以上简谐振动的合成。这种研究方法,为我们研究一切复杂振动奠定了坚实的理论基础。

2.5.2 一个物体的简谐振动

一个物体的简谐振动分两种情况,一种是自由振动,另一种是受迫振动。

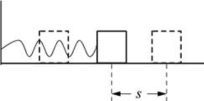
图2-38 弹簧振子

1.自由振动

(1)自由振动时,ΣF外=0,物体在外力起始作用下,一旦离开平衡位置以后就能够自行继续振动,不再需要外力的持续作用。我们通过自由振动中的弹簧振子、单摆和复摆这三个实例来说明,如图2-38～图2-40所示。

通过这三个实例,我们发现它们各自的运动方程体现出自由振动时的特征,这些运动方程是通过牛顿第二定律和刚体的转动定律推导而得到的。现在,我们把三个实例的运动方程都纳入一个共同的简谐振动的运动方程中:

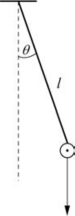
图2-39 单摆

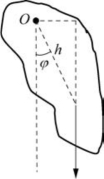
图2-40 复摆

式中,x在弹簧振子中表示位移s,在单摆中表示角位移θ,在复摆中表示角位移φ;t表示时间;ω2永远是正值,在弹簧振子中表示k/m,在单摆中表示g/l,在复摆中表示mgh/I(转动惯量)。

这三种运动受到的力被称为弹性力或准弹性力,都可看作振动系统的内力,力或力矩的大小与位移或角位移成正比但符号相反。

现在,我们可以为简谐振动下一个定义:像弹簧振子、单摆和复摆等由弹性力或准弹性力所引起的振动,或者说运动方程可纳入式(2-1)这种形式的运动,都称为简谐运动。根据微分方程理论,满足上述运动方程的解是:

x=Acos(ωt+α)或x=Asin(ωt+α')。

因此,能够满足上述方程的解的运动也是简谐运动

简谐振动的基本性质是它的周期性,我们用周期T频率ν和圆频率ω这三个物理量来描述;同时,又引进振幅A、位相(ωt+α)和初位相α这三个物理量;如图241所示。

另外,我们也能用几何的方法,即矢量图法来形象简便地表达简谐振动中位移和时间的关系,如图2 42所示。图中,矢量A在x轴中的投影x=Acos(ωt+α)就是给定的简谐振动。

物体在做简谐振动时具有能量,即动能和势能。若物体只受到内力中的弹性力或准弹性力作用(合称保守力),没有受到内力中的耗散力作用,也没有受到外力作用,这时的简谐振动的能量是守恒的。以弹簧振子为例,。、

图2-41 简谐振动物理量

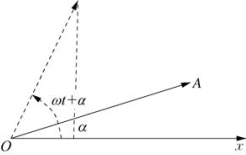
图2-42 简谐振动中位移和时间的关系

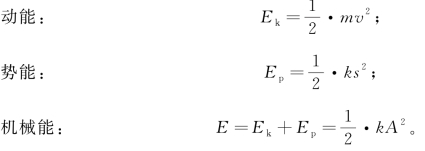
(2)阻尼振动

实际上,简谐振动总要受到摩擦阻力或黏滞阻力等外力的影响,所以能量是不守恒的。物体受到的总力为弹性力(或准弹性力)和阻力之和。阻尼振动是振幅随时间而减少的振动。以单摆为例,阻尼振动的运动方程式为:

式中,β称为阻尼因数,与系统本身性质和介质性质有关。随着阻力的大小不同,x的解可能出现三种情况(此处不做详细介绍)。

2.受迫振动

受迫振动时,ΣF外≠0,物体在外来周期性力的持续作用下才能持续振动。其运动方程式为:

式中,h=H/m,H为力幅(强迫力的最大值);f为强迫力,f=Hcospt;p为强迫力的圆频率。

3.几种振动的比较

①自由振动的运动方程式:

②阻尼振动的运动方程式:

③受迫振动的运动方程式:(www.xing528.com)

4.共振

当我们把简谐运动中的自由振动和受迫振动结合起来的时候,就出现另外几种现象。

①当强迫力的圆频率p比固有圆频率ω0大得多时,

A≈0,即:振幅很小。

②当强迫力的圆频率p比固有圆频率ω0小得多时,

A≈H/k,即:振幅相当于一个不变的力H加在振动系统上引起的位移。

③当强迫力的圆频率p等于物体做自由振动的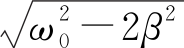时,物体的振动幅度会达到极大值,这种现象称为共振。

共振时的圆频率:

共振时的振幅:

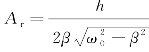
共振具有普遍性,对建筑物、桥梁和机器设备都会产生破坏作用。控制强迫力作用产生破坏的方法有:

①改变固有圆频率ω0的大小;

②改变阻尼因素β的大小;

③改变强迫力h的大小。

当然,共振也是可以利用的,例如:超声发生器、无线电接收器等。

2.5.3 两个物体的简谐振动

(1)在两个物体的简谐振动中,根据振动方向和振动频率可分为四种情况。

①方向相同,频率相同。

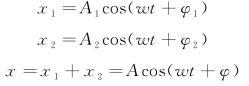
式中,x1、A1、ω、φ1分别表示第一个简谐振动的位移、振幅、圆频率和初相位;x2、A2、ω、φ2分别表示第二个简谐振动的位移、振幅、圆频率和初相位;x、A、ω、φ分别表示合成简谐振动的位移、振幅、圆频率和初相位。

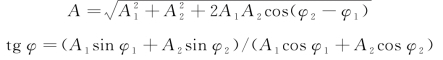
结果:合成的振动仍是一个简谐振动,合成振动的频率与原来的分频率相同,如图2-43所示。

②方向相同,频率不同。

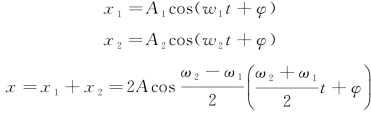
结果:合成的振动不是一个简谐振动,有时会合成时强时弱的振幅,这种现象被称为“拍”。

式中,ν称为拍频,即单位时间内振幅加强或减弱的次数,数值是两个分振动频率ν2与ν1之差。

图2-43

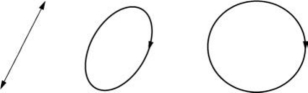
图2-44

③方向垂直,频率相同。

结果:合成的振动在一条直线、椭圆或圆上进行,如图244所示。

图2-45 利萨如图形

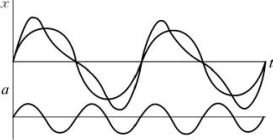
图2-46 振动分解

④方向垂直,频率不同。

结果:合成的振动比较复杂,而且轨迹不稳定。其中比较稳定的轨迹图形称为利萨如图形,如图2-45所示。

(2)两个简谐振动可以合成为一个简谐振动,这就是简谐振动的合成。反过来,任何一个简谐振动也都可以分解成若干个简谐振动,这就是简谐振动的分解。

傅里叶定理表明:任何一个周期性振动,都可以分解成若干个简谐振动,这些简谐振动的频率是原来振动频率的整数倍,如图2-46所示。同样,任何一个非周期性的振动也能够分解成若干个简谐振动,但是这些简谐振动的频率不再是原来振动频率的整数倍。

总而言之,我们可以把任意一个周期性振动或非周期性振动分解成若干个最基本的简谐振动,使复杂的问题归于简单。