刚体力学与质点力学联系及转动力矩

2.3.1 结构图

2.3.2 运动学

1.结构图

2.知识要点

(1)概述

刚体是在任何情况下,形状和大小都不发生变化的物体。平动和转动是刚体运动中最简单的两种运动,其他任何复杂的运动都可以看成是这两种最简单运动的合成。这种分析思路是具有真正的科学意义的,是所有科学研究人员终身信奉的真理。

(2)刚体平动

图2-23 刚体平动

在刚体平动时,其中任意两点之间的直线a在各个时刻的位置始终彼此平行,如图2-23所示。图中,刚体上面的所有质点的运动是完全相同的,因此,所有描述质点运动的物理量,例如速度和加速度等都适用于描述整个刚体的运动。通过这种方式,我们把刚体力学和质点力学联系起来。

(3)刚体转动

刚体上的各点都绕一直线O1O2做圆周运动,直线O1O2叫转轴,这种运动叫刚体转动,如图2-24所示。如果刚体转动时,转轴O1O2固定不动,这种运动叫绕固定轴转动。如果刚体转动时,转轴O1O2上仅一点固定不动,这种运动叫绕固定点转动。

图2-24 刚体转动

以下的讨论,都围绕刚体绕固定轴转动展开。

①匀速转动

刚体上的一点在一段时间Δt内转过的角度Δφ,称为在Δt时间内的角位移。在任意相等的时间内,角位移相等的转动叫匀速转动。

角速度:w=(φ-φ0)/(t-t0)

角位移:φ=wt(当t0=0时,φ0=0)

角速度是矢量,有数值,有方向。

矢量的方向沿转动轴线的方向,矢量的指向与刚体绕轴线的转动遵循右手定则即由矢量的始端沿矢量看过去是顺时针的,矢量的长度表示角速度的数值。当刚体绕定轴转动时,如果轴的方向确定,根据右手定则,角速度的方向只有两种,即正或负。当刚体绕定点转动时,轴的方向可能变化,根据右手定则,角速度的方向常用矢量w表示,w的大小是dφ/dt。

②变速转动

在不相等的时间内,角位移相等的转动叫变速转动。平均角速度:

瞬时角速度:

③匀变速转动

在任意相等的时间内,角速度的改变都相等的转动叫匀变速转动。角加速度:

式中,角加速度是矢量,有数值,有方向。

④刚体上某一点的运动状态

A为刚体上的任意一点,在Δt时间内走过路程A1A2,即弧长Δs,转过的角度为Δφ,A点到转轴的半径为r,如图2-24所示。

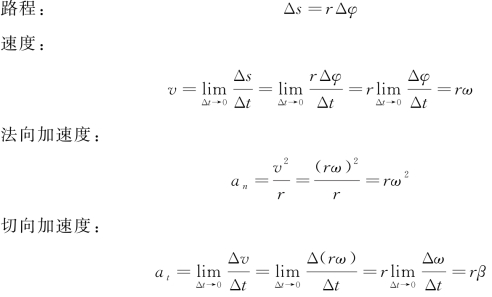
2.3.3 动力学

1.结构图

2.知识要点

再次强调:简略地说,运动学研究物体的运动,动力学研究物体的力和运动。

(1)刚体平动

物体可以看成是由无数的质量元组成,形成一个质点组,各质点之间的距离保持不变。物体的全部质点的运动和单独一个质点的运动相当。这时刚体的运动规律是:ΣF=ma。其中,F和a都是矢量。这个运动规律与质点动力学中的牛顿第二定律相似。

(2)刚体任意运动

刚体任意运动时的运动规律称为质心运动定律:ΣF=mac。

当刚体做任意运动时,质量和质心加速度的乘积等于作用在刚体上的外力的矢量和。其中,ac称为质心加速度。

式中,质心C表示刚体的质量中心,它的空间坐标由三维坐标系决定:

对于质量分布均匀而且形状对称的刚体,如圆环、圆柱、长方体等,它们的质心位于刚体的几何中心处,可能在刚体上(圆柱),也可能不在刚体上(圆环)。

质心运动定律只适用于刚体质心的加速度,不适用于刚体上每一个质量元的加速度。

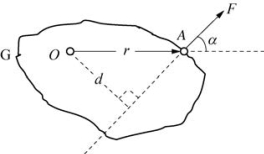
图2-25 刚体转动

(3)刚体转动(绕固定轴转动)

①力矩(相当于质点动力学中的力F)

图2-25中,刚体G可绕O轴转动(O轴垂直于纸面)。F为垂直于O轴的平面内作用于刚体上的外力。d表示外力F的作用线到轴线的垂直距离,称为力臂。r表示由轴指向外力F的作用点(A)的矢径。α表示r与F的夹角。

如果外力F不在垂直于O轴的平面内,我们可以把F分解为两个正交的分力,一个分力与轴平行,另一个分力在垂直于O轴的平面内。前者对刚体绕固定轴转动没有影响,故本章讨论的都是后者。(www.xing528.com)

力矩M的数值,是力F与力臂的乘积,即:

式中,力矩是矢量,它的方向垂直于r与F决定的平面内,在绕固定轴转动时,力矩的方向与轴线方向一致,它的指向由r与F组成的右手定则决定。

力矩M的矢量式:M=r·F

力矩的合成遵从平行四边形法则。

②转动惯量(相当于质点动力学中的质量m)

转动惯量是所有质量元与其半径的平方的乘积之和。

式中,I与刚体的质量有关,与质量的分布有关,还和轴的位置有关。

平行轴定理:

对于任一刚体,如果通过质心的轴的转动惯量为已知的IO,那么,任何一个与该轴平行的其他轴的转动惯量Ic(如图2-26所示)为:

式中,m为刚体质量;d为两轴之间的垂直距离;Ic＞IO。

图2-26

图2-27

垂直轴定理:

垂直于刚体的z轴的转动惯量为Iz,与它正相交的x轴和y轴的转动惯量分别为Ix和Iy,如图2-27所示,则:

Iz=Ix+Iy

③转动定律(相当于质点动力学中的牛顿第二定律)

由于刚体绕固定轴转动,所以它的运动规律就必然有其本身的特征:

牛顿第二定律:ΣF=ma

式中,ΣF为合外力,m为质量,a为加速度。

刚体转动定律:M=Iβ(矢量式)

式中,M为力矩,I为转动惯量,β为角加速度。

通过类比,在我们学习了质点动力学后,再研究刚体力学中的有关内容就容易多了。

图 2-28陀螺的进动

(4)角动量和冲量矩

①角动量(相当于质点动力学中的动量mv)

Lz=Izw

②角动量定理(相当于质点动力学中的动量定理)

角动量定理的应用:陀螺的进动现象,如图2-28所示。

③角动量守恒定律(相当于质点动力学中的动量守恒定律)

ΣIω=常量

④冲量矩(相当于质点动力学中的冲量Ft)

(5)功和能

①力矩功(相当于质点动力学中的功)

②动能(相当于质点动力学中的动能)

③动能定理(相当于质点动力学中的动能定理)

式中,力矩功等于动能增量。

④重力势能(相当于质点动力学中的重力势能)

⑤机械能(相当于质点动力学中的机械能)

⑥功能原理(相当于质点动力学中的功能原理)式中,除重力以外的其他外力的合力矩所做的功等于刚体机械能的增量。

⑦机械能守恒定律(相当于质点动力学中的机械能守恒定律)