万有引力的本质：以太振动引起的粒子偏转

我们通过粒子—光子模型与暗波模型推导出引力场的产生机制，再考虑到以太海密度对光速的影响，以及粒子与光子的以太结构，我们现在就可以在“物质以太”的观念下对万有引力做出解释。

现在，让我们想象空间中出现了一个有质量的粒子，或者一个大质量天体，那这个天体附近以太海的密度就不再均匀，距离天体越近的空间位置上，以太海的可用密度越低，光速也越低。

然后，我们想象一个光子从天体下方掠过这个天体附近的空间。

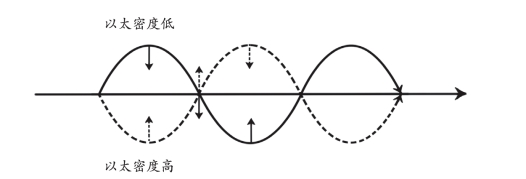
图9-1　光子振动与以太海密度的关系示意图

在以太观念下，光子可以看作正负以太元素的振动与前行。光子前行的速度是c，这与以太海的密度有关，而光子中正负以太元素在垂直方向上的振动速度也必然与以太海的密度相关。

如果在光子经过的空间中，以太海密度是均匀的，那上图横轴的箭头即为光子的运动轨迹，构成光子的正负以太元素上下振动的幅度相同，所以当光子中的正负以太分散再聚合时，聚合点仍然会落在横轴上。这个光子会保持原来的运动方向不变，光子前行的路径是直线，如图所示。

如果因为这个大质量天体的存在，导致光子途经的空间中以太海的密度不同，靠近天体的方向上以太海的密度更低，即在坐标轴上方振动的正（负）以太元素的速度低于坐标轴下方的负（正）以太元素的速度，就会导致其分离后再聚合的位置点发生改变。

在这个例子中，由于是从质量粒子下方掠过，光子在原光路上方振动的以太成分的速度，要低于原光路下方振动的以太成分的速度，所以当在原光路下方振动的那部分以太成分回到原光路时，在上方振动的那部分以太成分还没有返回，这使得在原光路下方振动的那部分以太成分还需要继续向上移动才能聚合在一起，完成光子中正负以太元素的一次振动。(www.xing528.com)

因此，在一次振动结束后，这个光子的位置会偏离原本的方向，而随着光子的前行与持续振动，这个光子会向以太海密度更低的方向（即大质量天体所在的方向）发生偏转。

一个光子如此，由光子形成的粒子同样如此。随着粒子内光子的波动，粒子也会向以太海密度更低的方向偏转。

粒子会因为其内部正负以太元素的振动，逐渐向以太海密度更低的方向偏转，这正是以太假说下万有引力的本质。

这个过程中同样会有能量的转移。因为粒子出现了位移与速度上的变化，它需要获得更多的能量，所以它会从以太海中获取与之匹配的以太元素，这也是重力势能向动能转化的过程。

以上，就是为什么在质量粒子周围会出现引力场，而引力场又会对其中的粒子产生万有引力、重力势能转化为动能的全部过程^[2]。

在第六章我们谈到过粒子的惯性质量，我们发现其与粒子内部光子的能量，或者说以太数量相关。现在，我们可以确认引力质量也是如此。因为无论是惯性质量还是引力质量，其本质都是粒子中以太元素的运动，它们都与在粒子内部运动着的以太元素的数量相关。

只不过在讨论惯性质量时，我们更侧重粒子的以太结构，以及粒子内以太元素与以太海中以太元素之间的相互作用。而在讨论引力质量时，我们会强调以太海的波动，也就是暗波机制。

因此，在“物质以太”的观念下，所有力都可以被描述，能量的转移更是如此。我们同样可以确认，万有引力的确与电磁力有不同的产生机制，很难被标准模型用一种数学表述来统一。