现代燃烧和爆炸理论中的爆轰波关系解析

为了进一步阐述经典的爆轰波流体力学理论，以多方气体中的爆轰为例进行讨论。对于多方气体，其内能可表示为

根据能量守恒方程，多方气体爆轰波的Hugoniot方程可写为

对式（14．21）进行变换可得

或

将Rayleigh线方程（14．5）写成如下形式：

引入爆轰波相对初始气体的马赫数Ma0=，并考虑到多方气体的初始声速，则式（4．23）可改写为

将式（14．24）代入式（14．22）后得到：

将式（14．25）看成的形式，可求得其一阶和二阶导数分别为

显然在f′=0 时有极值，又因为f″>0，所以函数在f′=0 处取极小值，该极小值出现在

对上式进行分析，可以得到以下三种情况：

当Ma20=1时，=1；

当Ma20>1时，<1；

当Ma20<1时，>1。

在爆轰情况下，始终有，因而也始终有Ma20>1，即

上式表明爆轰波的速度相对波前介质是超声速的。(www.xing528.com)

如果对式（14．26）进行求解可以得到

式中，。

由质量守恒可得

由此可得

式中，Ma为爆轰波相对波后产物的马赫数；c为爆轰波后产物中的声速。

将式（14．24）和式（14．30）代入式（14．31）得

对式（14．32）进行分析，可以得到以下三种情况：

（1）当根式项取零时，有唯一解且对应CJ爆轰的情况，解得Ma=1，即=1。故有

（2）当根式前取正号时，有Ma2>1，则有

此时与弱爆轰情况相对应。

（3）而当根式前取负号时有Ma2<1，故有

此时与强爆轰相对应。这是因为弱爆轰时产物的比容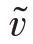比强爆轰时要大，但压力p 却比强爆轰小，由式（14．33）可知，强爆轰的Ma值要比弱爆轰的Ma值小。

由式（14．30）、式（14．33）、式（14．35），可以得出以下结论，即爆轰波相对波前介质是超声速的；相对于波阵面后的介质而言，强爆轰是亚声速的，弱爆轰是超声速的，CJ 爆轰是声速的。这个结论称为Jouguet法则。