涡破碎和涡耗散模型-现代燃烧和爆炸理论

Spalding早在1971年就尝试对湍流燃烧控制方程中的化学反应源项（见式（13．58））提出封闭条件。基于湍流混合中能量级串的思想（详见13．3．3节），即大尺度湍涡会将它的能量传递给邻近的较小尺度的湍涡而非直接将其耗散成热，这种过程被假定一直重演下去，直至达到Kolmogorov尺度η，在更小的尺度能量通过黏性作用直接弥散成热。如果化学反应特征时间远小于湍流流动时间，以上控制湍流混合的级串过程是决定反应的关键过程，即化学反应速率取决于未燃烧气体微团在湍流作用下破碎成更小微团的速率。这一模型被称为涡破碎模型（Eddy Breakup Model，EBM）。湍流的产物平均生成率为

式中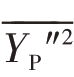，是产物质量分数的方差；CEBU是涡破碎常数。

Magnussen和Hjertager（1977）用贫燃料混合物中的燃料或者富燃料混合物中的氧化剂的平均质量分数代替，将涡破碎模型改进为涡耗散模型（Eddy Dissipation Model，EDM）。涡耗散模型利用燃料、氧化剂和燃料的平均净反应率中的最小值来计算化学反应源项(www.xing528.com)

式（13．72）中的A、B是拟合参数，ν是等化学计量质量比。

涡破碎和涡耗散用湍流流动时间τ=代替一步反应近似中的化学时间尺度，因此这些模型不能考虑化学反应动力学的影响，也就是说考虑的是无限快速反应的极限情形。尽管模拟结果和实际差别较大，但由于此模型简单直观，目前在商用软件如FLUENT、STAR-CD、CFX等中仍然广泛使用此模型。