现代燃烧和爆炸理论：雷诺平均湍流模型解析

本节中我们首先介绍基于单点平均的Navier-Stokes 方程，一般被称为雷诺平均Navier-Stokes方程（Reynolds Averaged Navier-Stokes Equations，RANS）。通过上节中引入的Favre平均，将RANS模型扩展到密度变化的湍流流场。然后重点介绍对于湍流流场分析最为重要的简化模型，即k-ε模型。RANS模型是求解工业燃烧流场最常用的方法，尽管k-ε模型对流场的预测能力（除了简单剪切流）往往与实际情况相差甚远，但k-ε模型仍然提供了对于湍流流场至关重要的湍流长度和时间尺度。

对于可压缩流场，Navier-Stokes方程组包含的守恒方程有：

连续性方程为

动量方程为

式（13．25）等号左边的两项分别代表动量的局部变化率和对流项，而等号右边的三项分别代表压力梯度、黏性的分子输运和浮力效应。黏性应力张量τ与应变率张量S之间的关系为

其中，μ是动力黏性系数，μ与运动黏性系数ν之间存在关系μ=ρν。

对于式（13．24）和式（13．25）采用Favre平均可得

比较式（13．29）和式（13．25）可以发现，式（13．29）只比式（13．25）多了等号右边包含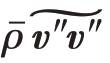的第三项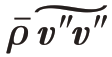，被称为雷诺应力张量。Favre平均湍动能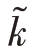为(www.xing528.com)

引入涡动黏性νt，则雷诺应力张量可以表达为

涡动黏性νt与Favre平均湍动能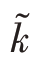存在以下关系：

其中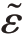，是Favre平均湍动能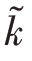的耗散率。Favre平均变量和需要各自的演化方程，最简单的模型为：

Favre平均湍动能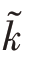

Favre平均湍动能的耗散率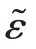

式（13．33）和式（13．34）等号左边的两项分别代表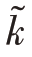和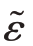的局部变化率和它们的对流项。式（13．33）和式（13．34）等号右边的三项代表湍流输运、湍流生成和湍流耗散。在一般的kε模型中，通常取σk=1．0，σε=1．3，cε1=1.44，cε2=1.92。