湍流的统计描述-《现代燃烧和爆炸理论》

湍流的统计表述方法是通过概率密度函数（Probability Density of Function，PDF）来表征脉动速度和标量场。以下以速度分量u为例来说明如何通过PDF来表征脉动速度。分布函数Fu表示随机统计变量u<U的概率p

u出现在区间U-<u<U+内的概率为

u的概率密度函数（PDF）定义为

Pu（U）dU就是u出现在区间U<u<U+dU内的概率。如果u的上下限分别为+∞和-∞，则

在湍流中，一般而言，任意统计变量的PDF都取决于位置x和时间t，因此PDF的形式一般表达为Pu（U；x，t）或P（u；x，t）。一旦某个任意统计变量的PDF已知，则该统计变量的矩定义为

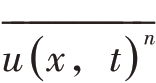代表u（x，t）n的均值，或者期望值。u的一阶矩即为u的均值

类似的，函数g（u）的平均值为

对于密度强烈变化的流场，经常采用密度加权平均的速度，即Favre均值。将随机统计变量u（x，t）分解成（x，t）和u″（x，t）：

Favre平均方法要求u″（x，t）和密度ρ的乘积均值为零，即

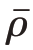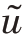因此，ρu的均值等于ρ的均值乘以，即(www.xing528.com)

如果瞬时的ρ 和u 已知，采用式（13．15）就可以得到密度加权的。在密度变化（可压缩）流场中，即使瞬时的ρ和u很难获取，Favre平均方法在简化平均Navier-Stokes 方程上仍具有极大优势。高雷诺数流动中，动量、能量和组分守恒方程中对流项占主导，此时黏性和输运项是次要项。对于对流项ρuv的平均会出现四项：

其中

而采用Favre平均，ρuv可以表达为

式（13．18）中并没有出现密度的脉动项。考虑到式（13．13），ρuv 的Favre 平均仅出现两项

式（13．19）的表达式明显比式（13．16）简化。在密度不变时，式（13．19）退化成与式（13．16）同样的形式，此时

引入密度加权的Favre平均需要知道密度和需考察变量之间的相关性，变量u的Favre PDF可以通过联合概率密度函数P（ρ，u）得到

式（13．21）等号两边乘以u然后积分得

式（13．22）等价于，因此Favre均值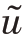可以定义为