输运系数微观起源及其在现代燃烧和爆炸理论中的应用

从分子热运动的角度而言，气体的黏度是分子的随机运动和分子在z方向的碰撞产生的动量交换。考虑速度为v=（vx，vy，vz）的气体分子，在空间位置z′处发生第一次碰撞，在空间位置z处发生第二次碰撞。两次碰撞之间分子运动的路程为平均自由路径λg。因此

其中，

假设分子在第一次碰撞后，周围流场达到了局部均衡。分子在第一次碰撞后携带的动量等于

将p（z′）展开为如下形式

空间点z′处速度为v的分子数量为

其中N是空间点z′处的分子总数密度，fv（vx，vy，vz）为玻尔兹曼速度分布，且有

式中，m 是分子质量；k 是两分子碰撞的频率系数；kB是玻尔兹曼常数。这些分子在x 方向上的平均速度非零，于是玻尔兹曼能量分布写成

穿过z′的分子通量为

每一个分子携带的动量为p（z′）。对整个速度空间积分可以得到通过z′的净动量流通量：

忽略式（5．44）的高阶项，将其代入式（5．49），可得

式（5．50）等号右边的第一个积分项为零。对于第二个积分项，由于vx与气体中的声速量级相同，而流场速度u（z）远小于声速，因此u（z）≪vx，第二个积分项可以简化为

其中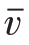，是气体的平均速度，且

由于动量与平均速度成正比，即有

将式（5．53）代入式（5．51）可得

对比式（5．54）与牛顿黏性定律

可以得到黏度的近似公式(www.xing528.com)

从上述公式可以得知，黏度与压力无关。

上述关于黏性的计算流程也适用于热传导性。此时需要将动量替换为显焓T，动量流通量替换为热量流通量

式中，Navg为阿伏伽德罗常数。对比傅里叶热传导定律

于是热传导率λ近似为

式（5．59）表明，热传导率与比热容，以及分子随机运动的平均速度成正比，与碰撞截面成反比，与压力无关。

式（5．59）只是一个近似计算，因为它没有考虑到高温区域中较热的分子与低温区域中较冷的分子之间碰撞导致的能量传递。分子碰撞对于热传导的影响需要更严格的论证，尽管分子碰撞中会发生能量转移从而促进热传导，但是分子碰撞使得冷分子阻止了热分子向低温区域运动，进而削弱了热传递。

最后，我们采用与推导黏度和热传导性的近似公式类似的方法来推导二元组分扩散系数。一个测量二元扩散系数的理想试验是将两种不同气体（组分1和组分2）充满一根管道，管道的轴向作为z轴，并在z方向维持某个浓度梯度，单位体积的气体分子总数不变

在z′处刚完成一次碰撞时的分子数密度为

穿过垂直于z轴的单位截面积的分子总数约为

在上述公式中，分子的平均自由程为两种不同气体分子平均自由程的平均值。在整个速度空间上对式（5．62）进行积分，可以得到组分1分子的净流量

比较费克扩散定律，有

由于类型1和类型2的分子拥有几乎相同的碰撞直径，于是有

由此可知，二元扩散系数与密度或压力成反比。

式（5．56）、式（5．59）、式（5．65）是实用的，因为它们给出了黏度、热传导率、扩散系数与温度和压力的依赖关系（如果关系存在的话）。想要对这些运输系数进行更加严密的处理，必须考虑碰撞能量转移以及分子间作用力的影响。