跨流域调水工程水污染应急调控技术与应用

3.2.2.1 分水口边界条件

分水口处渠道的流量会有变化,相应水位也会有变化,以横向流出分水为例如图3.2所示。

图3.2　分水口示意图

图3.2中,j、j+1分别为分水口上下端的断面的编号,分水口上端流量为Qj,下端流量为Qj+1,分水的流量为Qf,则有水量平衡和能守恒可得

式中:Zj为分水口上端渠道底高程。

对式(3.43)、式(3.44)做泰勒级数展开整理得

则式(3.45)、式(3.46)可以分别写成式(3.18)、式(3.24)的形式。其系数为:a2j=0;b2j=1.0;c2j=0;d2j=-1.0;e2j=+Qf;a2j+1=1-

3.2.2.2 渐变段边界条件

如图3.3所示,过水断面增大或者缩小的情况,有以下相容条件:

式中:ζ为局部损失系数;ξ为其他损失系数。

对式(3.47)、式(3.48)线性化处理得

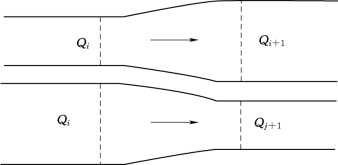
图3.3　渐变段示意图

式(3.50)、式(3.51)分别是渐缩、渐扩段的能量方程。则式(3.49)、式(3.50)、式(3.51)可以写成式(3.18)、式(3.24)的形式,其系数为:a2j=0;b2j=1.0;c2j=0;d2j=-1.0;

渐缩段系数:

渐扩段系数:

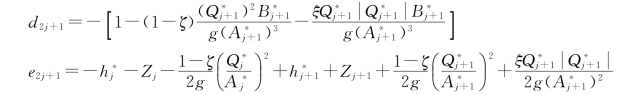
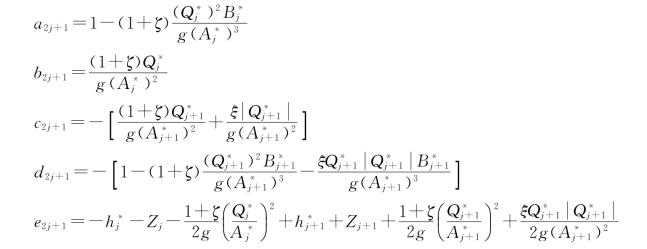
3.2.2.3 倒虹吸边界条件

参照南水北调中线总干渠的设计资料,干渠上80%以上的倒虹吸长度都小于1000m。对于这种尺度的倒虹吸管涵,可以对渠水波动在其中的传播时间做一个简单的估算,以西赵河倒虹吸为例。该倒虹吸为4孔并联形式,单孔尺寸为6.9m×6.9m(宽×高),设计流量为340m3/s,加大流量为410m3/s,倒虹吸的长度为300m。

在管道非恒定流水力学中,水击波速的计算公式如下:

式中:c为管道中的水击波速;K为水的体积弹性系数,取2.39×109;σ为水的密度,其值为1×103 kg/m3;E为管道壁的弹性系数,在本次研究中取混凝土的弹性系数,为30×109;D为管道壁的等效半径,其值为3.9m;e为管壁厚度,取0.5m。

计算得:c=953.47m/s。水击波速在该倒虹吸中管涵中的传播时间约为0.31s。这个时间相对于明渠计算时间步长Δt来说,可以忽略不计。因此在计算非恒定流时,两节点间的水位差为倒虹吸进口、出口的局部水头损失和中间的沿程水头损失之和,则满足以下连接条件:

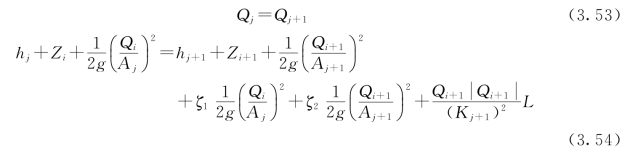
式中:L为倒虹吸的长度。

对式(3.53)、式(3.54)线性化处理得

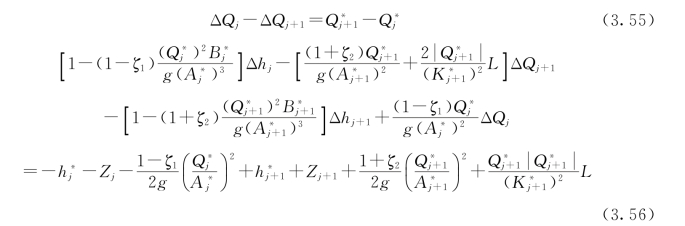
式中:K=

则把式(3.55)、式(3.56)化简成式(3.18)、式(3.24)的格式,其系数为:a2j=0;b2j=1.0;c2j=0;d2j=-1.0;e2j=;a2j+1=1-(1-ζ1)×

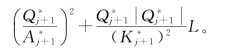
3.2.2.4 节制闸边界条件

一维明渠流数学模型中,为了保证计算时候的连续性,人们通常将节制闸作为内边界来处置。

如图3.4所示,南水北调中线总干渠上全部采用弧形闸门,从物理意义上分析,节制闸的过流能力方程应该是一个3段连续函数,即孔流段、过渡段、堰流段。在过渡段的两端点,分别与孔流段、堰流段的函数是连续的。有必要做相应的处理,以确定适用于渠道控制的过闸流量公式。过渡段计算采用孔流与堰流关于闸门开度的线性插值。

图3.4　弧形闸门示意图

令K=,e为闸门开度,H0为闸前水位。过渡态的两端有两个点:①孔流分界点K1;②堰流分界点K2。不同的流态K1、K2的值也不同,有一定的变动范围。生产中,应允许取用不同的数值。当＞K2时为堰流,则堰流公式如下:

式中:σc为侧收缩系数;σs为淹没系数;m为流量系数;b为闸孔或堰的宽度;H0为闸前水深。

在使用堰流公式的时候,关键是选择合适淹没系数和流量系数。

(1)σs为宽顶堰的淹没系数,设Zd为为堰顶高程,H0为堰上游水位,H2为堰下游水位,(H2-Zd)/(H0-Zd)为淹没度。淹没系数采用巴普洛夫斯基实验数据,见表3.1。

表3.1　宽顶堰淹没系数表

当淹没度小于0.8时,淹没系数σs=1.0。

(2)m为宽顶堰的流量系数。采用有坎堰公式为

式中:A为闸室过水断面面积;H为堰前水深。

对于多孔闸门则需要计算综合流量系数,本书采用流量修正系数α进行修正,流量修正系数α的大小有实测水位水流进行修正。

(3)σc为侧收缩系数。对于平底闸门一般不考虑侧向收缩,而对于有底坎的宽顶堰,可用别列津斯基公式计算侧向收缩系数:

式中:Zd为堰底高;H为堰前水深;b为两墩的净宽;B为上游渠道的宽度;α为墩头和宽顶堰进口边缘形式有关的系数。

别列津斯基公式的使用条件为:≥0.2;≤0.3;当≤0.2时,取=0.2;当≥0.3时,取=0.3。

当＜K1时为孔流,闸孔出流时,根据闸门下游形成的水跃形式,其流态可以分为自由出流和淹没出流两种形式。

则闸孔出流公式如下:

式中:σc为侧收缩系数;σs为淹没系数;m为流量系数;b为闸孔或堰的宽度;H0为闸前水深;e为闸孔开度。

(1)m为闸孔的流量系数。

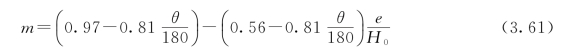
式中:θ为弧形闸门底的切线与水平方向的夹角,(°)。

公式的使用范围:25°≤θ≤90°,0.1≤≤K1。由cosθ=,0≤e≤emax,由此可以确定θ的取值范围。当＞K1时,认为是过度态或者堰流。

(2)σc为侧向收缩系数。

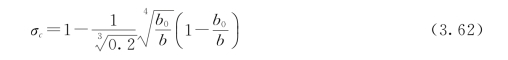(www.xing528.com)

式中:b0为闸室净宽;b为上游渠道中宽(水深一半处的宽)。

由于σc是的增函数,且不大于1。因此,当≥1时,σc=1;0.2≤＜1时,σc=1-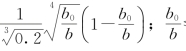≤0.2时,0.085。

(3)σs为淹没系数。

自由出流时σs=1。淹没出流状态时,先计算闸门处收缩断面水深hc,hc=εe,其中ε为垂直收缩系数,e为闸门开度。

再计算hc的共轭水深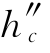

计算潜流比λ,λ=,H2为下游水深。若λ＜0,为自由出流,即σs=1;若λ＞1,下游水深高于上游水深,闸门上下游变换位置,重新计算,此时水倒流。0＜λ≤1,则采用《水闸规范》的表(A.0.3-2)的插值公式计算σs=-1.7823λ3+2.3338λ2+1。

当K1＜＜K2时,为过渡态,此时孔流的上线流量为Qkong,堰流的下限流量为Qyan,其中Qkong是有孔流公式计算得到,Qyan是有堰流公式计算得到。此时,过渡态的流量为

综上所述,节制闸无论是孔流、过渡态、堰流,在节制闸处都具有以下连接方程:

式中:σc为侧收缩系数;σs为淹没系数;m为流量系数;b为闸孔或堰的宽度;Hj为闸前水深;Hj+1为下一位置的闸前水深;e为闸孔开度。

对式(3.66)、式(3.67)进行泰勒级数展开,并整理得:

式中:f*=σcσsmbf(,e)。

式(3.68)、式(3.69)可以写成式(3.18)、式(3.24)的形式,其系数为:a2j=0;b2j=1.0;c2j=0;d2j=-1.0;

3.2.2.5 闸门参数识别

南水北调中线工程于2014年12月12日开始正式通水,距今已有两年多,目前运行状态均为闸孔淹没出流。利用工程实际运行中64座节制闸的大量原型观测数据来确定各节制闸的流量系数,可为工程运行调度和输水控制提供技术支撑,具有重要的实际意义。本文引进系统辨识方法,应用一种数学优化技术——最小二乘法,推导出通用的流量系数的计算公式,结合原型观测数据,可以快速便捷的求解流量系数。

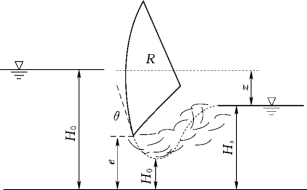
图3.5　闸孔淹没出流示意图

如图3.5所示,当闸门相对开度(e/H0)不超过0.65时为闸孔出流;当弧形闸门下游水深大于收缩断面水深的共轭水深时,闸孔为淹没出流。如前文所述,弧形闸门过闸流量计算各方法应用条件各异,关键是在流量系数等相关系数的确定。流量系数是一个与上下游水深和闸门开度等多因素相关的函数,由于其表达形式的复杂,多是基于一定条件简化后,采用流量系数曲线图(图3.6)或经验公式来确定,而其精度取决于流量系数曲线图拟合的公式或经验公式的阶数和各参数取值的影响,应用范围不具有通用性。结合工程实际条件,本书主要应用以下两种弧形闸门过闸流量计算方法,并提出了流量系数的系统辨识方法。

图3.6　淹没系数图

1.传统方法

赵昕等编著的《水力学》中闸孔淹没出流的流量计算公式为

式中:σs为淹没系数;μ为流量系数;n为闸孔数;b为孔宽,m;e为闸孔开度,m;H0为闸门全水头,m。

流量系数的计算公式为

式(3.71)的使用范围为:25°≤θ≤90°,0.1≤e/H0≤0.65。

式中:θ为弧形闸门底的切线与水平方向的夹角,°,由式(3.72)确定。

式中:c为弧形门转轴与闸门关闭时落点的高差,m;R为弧形门的半径,m。

流量系数的计算公式为

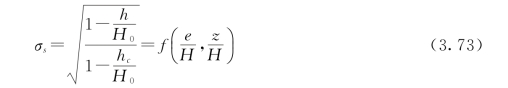
淹没系数σs具体表达式复杂,一般以z/H0和σs为纵横坐标,以e/H为参数,画出淹没系数曲线(图3.6)供查用。本文建立z/H-e/H-σs关系表,形式见表3.2,结果见表3.3(数值从图3.6中近似读出);然后利用线性插值的方法求得淹没系数。

表3.2　z/H-e/H-σs关系表

表3.3　z/H-e/H-σs关系表数值

假设某弧形闸门当前工况具有数值z/H和e/H,由z/H-e/H-σs关系线性插值可得到对应的淹没系数σs。若(z/H)i≤z/H＜(z/H)i+1,(e/H)j≤e/H＜(e/H)j+1,则σs的值由式(3.71)求得。

式中:(σs)i,j为(z/H)i和(e/H)j对应的淹没系数;(σs)i+1,j为(z/H)i+1和(e/H)j对应的淹没系数;(σs)i,j+1为(z/H)i和(e/H)j+1对应的淹没系数;(σs)i+1,j+1为(z/H)i+1和(e/H)j+1对应的淹没系数。

2.系统辨识法

本书使用的闸孔淹没出流的流量计算公式为

式中:Q为流量,m3/s;n为孔数;b为孔宽,m;e为开度,m;H0为闸前水深,m;Hs为闸后水深,m;C为流量系数。

传统方法和系统辨识法的差别主要体现在:传统方法分为淹没系数和流量系数,淹没系数将闸后水深因素囊括进去;而系统辨识法中用统一的流量系数包含了众多因素,应用最小二乘法来推导流量系数的计算公式。最小二乘法是通过最小化误差的平方和寻找数据的最佳函数匹配,可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。

在南水北调中线工程实际运行中,式(3.75)中的Q、n、b、e、H0和Hs均可进行原型测量;仅C为未知数。令

则式(3.76)可变为

则在式(3.76)中,Q和a为已知量,C为未知量。显然可知,可以得到一系列成对的数据(a1,Q1;a2,Q2;…;an,Qn)。将这些数据描绘在x-y直角坐标系中,理论上应在通过坐标原点的一条直线附近。可以令这条直线方程为

式中:C为任意实数,具体到闸门过闸流量计算上,C∈(0,1)。

应用最小二乘法原理,将流量实测值Qi与计算值yi(yi=Cai)的偏差的平方和(Qi-yi)2最小作为优化依据。令

则有

将s对C求导数,得

当s最小时,=0。即

因此,流量系数的计算公式为

即选择n个实际工况后,则可计算出流量系数C。