多元回归分析简介-基于R的数理统计学

在实际问题中，影响一个量y（称为因变量）的因素（称为自变量）往往有多个，例如，影响化工产品产出率的因素有反应温度、反应时间等；影响一种商品的销售量的因素有人均年收入、该产品的价格、相关商品的价格等。我们把研究一个因变量与多个自变量之间相随变动的定量关系问题称为多元回归问题。通常考虑因变量关于自变量的线性关系，即多元线性回归问题。虽然多元回归比一元回归应用更广泛、方法更复杂，但其基本原理与一元回归相类似，因而可看作是一元回归分析的一种扩展。前几节中讨论的一元回归分析的很多方法和概念对于多元回归问题仍然适用，但在计算和理论上较复杂一些。为此需要利用矩阵这一代数工具，使得叙述更方便，公式表达更简洁。本节并不打算对多元回归的理论方法等作详细介绍，只是对多元回归的模型和参数估计问题进行简单介绍。

本节考虑有p个自变量x1，x2，…，xp的情形。多元线性回归模型为

同时假定自变量是可控制的，即可视为非随机变量，其中b1，b2，…，bp分别称为y对x1，x2，…，xp的回归系数，ε仍为随机干扰项。

现设对x1，x2，…，xp和y进行了n次观察，得到n对观察值（xi1，xi2，…，xip，yi），i=1，2，…，n，ε1，ε2，…，εn是相应的随机误差，则基于样本的多元线性回归模型为

并假定ε1，ε2，…，εn相互独立，且同服从正态分布N（0，σ2）。令

则模型（6.6.2）可简写成

和一元回归分析一样，我们要根据观察所得数据对b0，b1，b2，…，bp，σ2进行估计。令

则b0，b1，…，bp的最小二乘估计应满足

即求b0，b1，…，bp使Q（b0，b1，…，bp）达到最小，为此令

得

这p+1个方程称为正规方程。

将式（6.6.4）进行整理，并用矩阵表示，即为

假定X′X可逆，在式（6.6.5）两边左乘（X′X）-1可得B的最小二乘估计

称为回归值。称为残差。

令

与一元线性回归类似，有如下定理。(www.xing528.com)

定理6.6.1 （1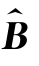）是B的线性无偏估计；

（2）s2是σ2的无偏估计；

（3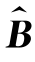）与s2相互独立。

证 （1）由于ε1，ε2，…，εn相互独立，且同服从正态分布N（0，σ2），因此E（ε）=0，根据式（6.6.3）得

E(Y)=E(XB+ε)=XB+E(ε)=XB

从而得

故是B的线性无偏估计。

（2）令P=I-X（X′X）-1X′，则有P′=P，P2=P，且P的迹

tr(P)=tr(I)-tr(X(X′X)-1X')=n-tr(X′X(X′X)-1)=n-p-1

易见P（XB）=0，而由式（6.6.8）知，e=PY，因此e=PY=PY-PXB=P（Y-XB）=Pε，这样

从而与一元线性回归一样，还需检验如下假设：

H0：b1=b2=…=bp=0 H1：b1，b2，…，bp中至少有一个不为零

若拒绝原假设H0，则说明多元回归模型线性效果显著；反之，回归方程并无实际意义。除此之外，还需对单个回归系数进行检验，即检验：

H0j:bj=0 H1j:bj≠0

若拒绝H0j，则说明xj对y的线性影响显著；反之，说明xj对y的影响较小，应从回归方程中予以剔除，并重新计算回归方程，这实际上是对变量进行筛选。逐步回归分析就是讨论这样的问题。另外，和一元回归分析一样，可根据所得回归方程进行预测。对此，本书不再一一加以介绍。