基于R的非线性回归模型-化为线性回归

前几节讨论了两变量之间的内在关系为线性关系时，如何拟合回归直线。但是，在实际中有时两变量之间的内在关系是非线性关系，即E（y|x）=f（x；θ1，θ2）是非线性的。一般来说，确定两变量之间的函数关系通常有两种方法：一种方法是根据专业知识，通过理论推导或根据经验来确定函数类型，例如细菌培养实验中，每一时刻的细菌总量y与时间x有指数关系，即y=a ebx；另一种方法是在根据理论和经验无法推知x和y间的函数类型的情况下，只能根据试验数据选取恰当类型的函数曲线来拟合。在拟合曲线时，最好用不同函数类型计算后进行比较。希望所拟合的曲线与观测数据（xi，yi）（i=1，2，…，n）拟合较好，通常用残差平方和

或相关指数

衡量拟合曲线的好坏，其中，且S2e越小或R2越大，表明拟合效果越好。

在某些情况下，针对所选取的函数，可以通过适当的变换，将变量间的关系式化为线性形式，举例如下。

（1）双曲线，如图6.5.1所示。

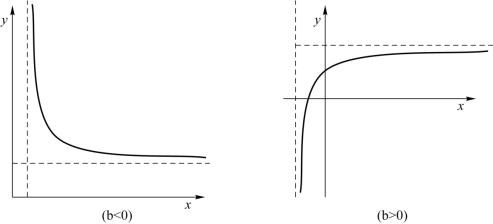
图6.5.1　双曲线

令，则

y'=a+bx'+ε,ε～N(0,σ2)

（2）幂函数曲线y=dxbε，lnε～N（0，σ2），如图6.5.2所示。

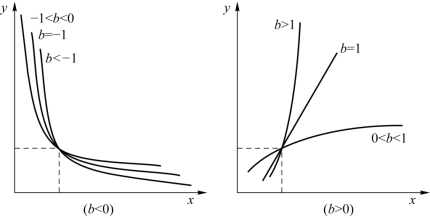
图6.5.2　幂函数曲线

令y'=ln y，x'=ln x，a=ln d，ε'=lnε，则

y'=a+bx'+ε',ε'～N(0,σ2)

（3）对数曲线y=a+bln x+ε，ε～N（0，σ2），如图6.5.3所示。

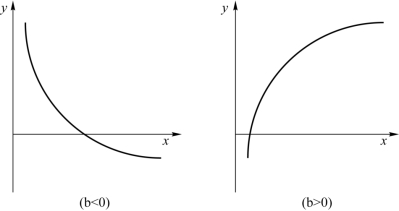
图6.5.3　对数曲线

令x'=ln x，则

y=a+bx'+ε,ε～N(0,σ2)

（4）指数函数曲线y=d ebxε，lnε～N（0，σ2），如图6.5.4所示。

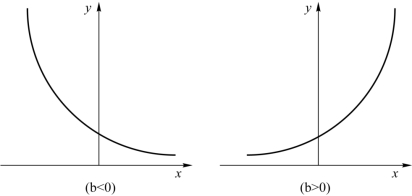
图6.5.4　指数函数曲线

令y'=ln y，a=ln d，ε'=lnε，则

y'=a+bx+ε',ε'～N(0,σ2)

（5）S形曲线，如图6.5.5所示。

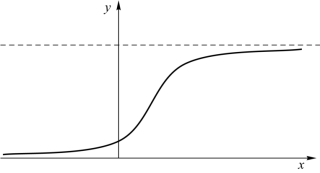
图6.5.5　S形曲线

令，则(www.xing528.com)

y'=a+bx'+ε,ε～N(0,σ2)

例6.5.1 为了考察某市百货商店的销售额x与流通费用率y之间的关系，表6.5.1列出了该市9个商店的销售额与流通费用率的统计资料，求y关于x的回归方程。

表6.5.1　销售额与流通费用率数据

解 作散点图，如图6.5.6所示，从图可以看出y随x的增加而减少，它们之间大致成双曲函数关系或幂函数关系。

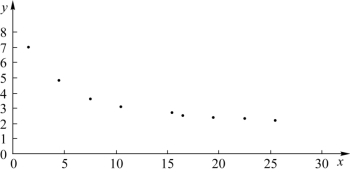
图6.5.6　销售额与流通数据散点图

先考察双曲线关系，即

令

则上式可写成y'=a+bx'，这是线性回归方程，从而可用最小二乘法估计a和b，经计算得

从而

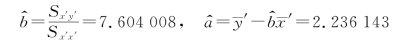
于是得回归方程

基于R的求解方法之一如下：

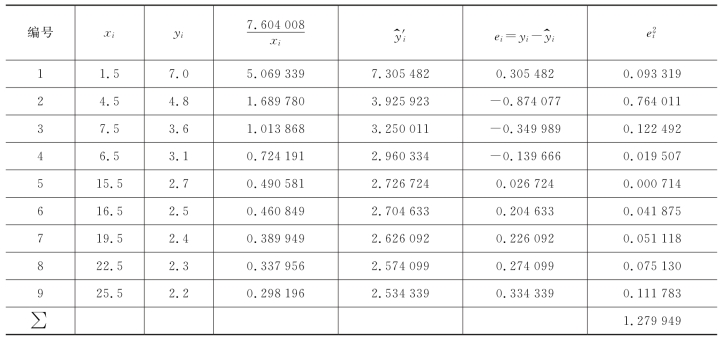
经检验，在显著性水平α=0.05下，回归方程（6.5.3）的线性关系显著，根据回归方程计算对应于各xi的回归值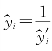，残差，以及残差平方和，具体计算如表6.5.2所示。

从表6.5.2中可以看出，残差平方和S2e≈1.28，总平方和Syy=20，相关指数为R2=1-，另外，销售额与流通费用的简单相关系数的平方为0.753 4，因此，两者是不同的。

表6.5.2　残差平方和计算数据表

基于R的求解方法之一如下：

再考察x与y之间的幂函数关系y=axb，得回归方程：y=8.520 972x-0.423293，残差平方和：S2e=0.007 021 2，相关指数R2=0.994 21。

基于R的求解方法之一如下：

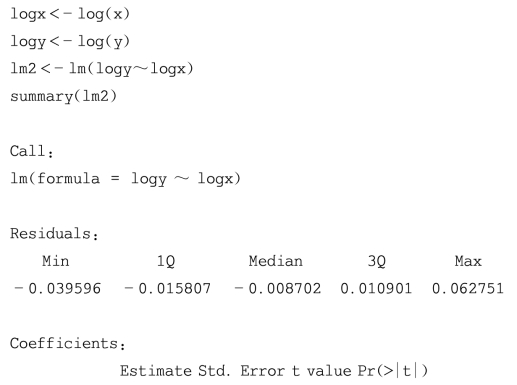
因此，拟合幂函数曲线比拟合双曲线的实际效果要好。另外，在对y进行预测时，可先对y'进行预测，再将y'的预测区间变换到y的区间。