基于R的数理统计学：求均值E（y0|x0）的置信区间

根据变量x和y的n对样本数据（xi，yi），i=1，2，…，n，拟合y对x的线性回归方程。假定通过检验，该回归方程线性显著。设当自变量x=x0时，因变量y的观测值为y0，则在线性回归模型（6.1.2）和（6.1.3）的假定下，

于是在x0处y的均值E（y0|x0）=a+bx0，而在x0处，y的回归值

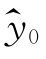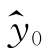其中由式（6.2.4）给出。很自然，取作为E（y0|x0）=a+bx0的估计值。由于均是y1，y2，…，yn的线性组合，则也是y1，y2，…，yn的线性组合。而y1，y2，…，yn相互独立，且yi～N（a+bxi，σ2），易证

因此

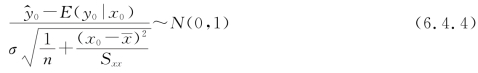
由式（6.2.13）和式（6.2.14）得

其中，S2是σ2的无偏估计。另外，由性质6.2.3知，相互独立，因此与独立，从而根据式（6.4.4）和式（6.4.5）得

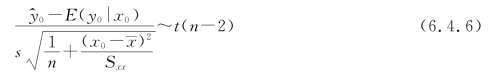
则有

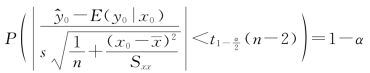(www.xing528.com)

从而E（y0|x0）的100（1-α）%置信区间为

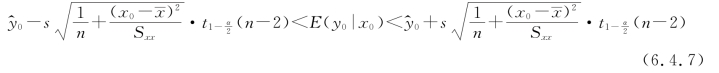
例6.4.1 设在例6.1.1的某类企业中，现有若干个企业均计划下个月产量为51台，求其单位成本均值的95%置信区间。

解 经计算得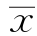=45.9，Sxx=7 380.7。由式（6.2.14）及表6.3.2得

查表得t0.975（28）=2.048 4，于是

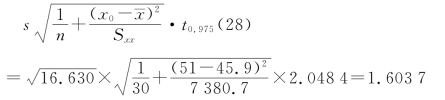
由式（6.2.8）得

由式（6.4.7）得，当x0=51时，单位成本均值E（y0|x0）的置信区间为（141.839 3，145.046 7）^[1]千元。

基于R的求解方法之一如下：