R语言实现的最小二乘法在数理统计学中的应用

在式（6.1.2）和式（6.1.3）的假定下，根据n对观测数据（xi，yi）（i=1，2，…，n）来估计模型中的参数a和b。若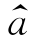和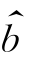分别是它们的估计，则对于给定的x，取作为y的估计。方程称为y关于x的线性回归方程，其图形为回归直线。直观上，应选择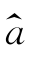和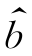使得所有数据点（xi，yi）（i=1，2，…，n）尽可能地靠近回归直线。记

称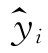为x=xi时y的回归值，称ei为残差，即观测值与回归值之差。

于是，e1，e2，…，en反映了数据点（xi，yi）对回归直线的偏离程度，我们当然希望这些偏离愈小愈好，衡量这些偏离大小的一个合理的单一指标为它们的平方和。令

参数a，b的估计值满足

为此，取Q分别关于a和b的偏导数，并令它们等于零。

方程组（6.2.3）称为正规方程。

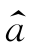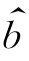解上述方程组得和，即

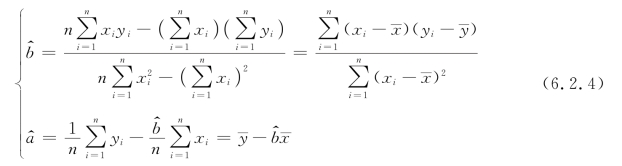
其中，

上述估计的原则是使误差平方和达到最小，因此，这种估计方法称为最小二乘估计法，式（6.2.4）确定的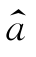和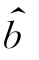称为a和b的最小二乘估计。

将代入线性回归方程得

式（6.2.5）表明回归直线经过散点图的几何中心。回归直线及各种图示如图6.2.1所示。(www.xing528.com)

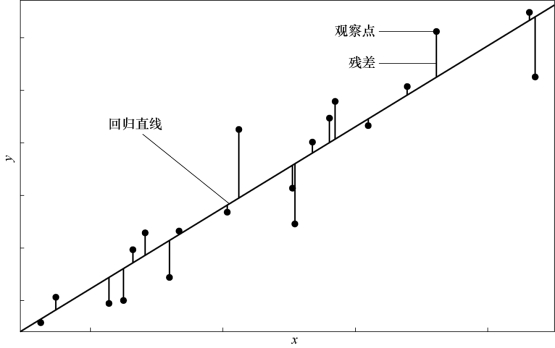
图6.2.1　回归直线的各种图示

为了计算方便，记

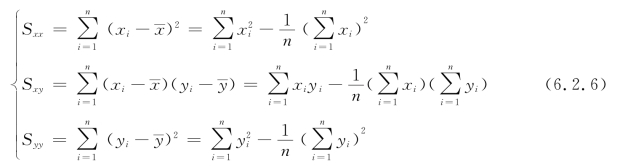
则

例6.2.1 根据表6.1.1给出的观测数据，确定y对x的线性回归方程。

解 画出散点图（如图6.2.2所示），根据式（6.2.6）得

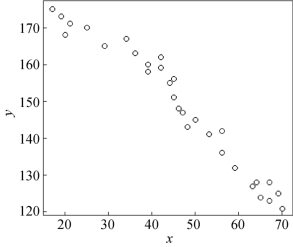
图6.2.2　某类企业产量（y）和成本（x）的数据圆圈表示的散点图

进而得

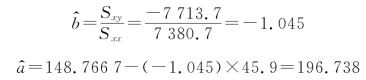
于是，线性回归方程为

基于R的求解方法之一如下：