基于R的单因素试验方差分析模型

设因素A有p个水平A1，A2，…，Ap。在水平Ai（i=1，2，…，p）下进行了n（n＞1）次独立试验，得到如表5.1.4所示的试验结果。

表5.1.4　单因素试验方差分析数据

在表5.1.4中，xij表示因素A取第i个水平时所得的第j个试验结果，xij不仅与因素A的第i个水平有关，而且受随机因素的影响。因此可将它表示成

xij=μi+εij i=1,2,…,p j=1,2,…,n

其中，μi表示在因素A取第i个水平下，没有随机因素干扰时本应得到的试验结果值，εij表示仅受随机因素影响的试验误差，它是一个随机变量。这样同一水平下的试验数据可以认为是来自同一个总体，并假定这一总体是服从正态分布，且对应于不同水平的正态总体，其方差是相同的。也就是说，对应于Ai的总体服从正态分布N（μi，σ2）。这样检验因素A对试验结果的影响是否显著就转化为检验p个正态总体的均值是否相等，即检验假设因此，单因素方差分析就相当于多总体均值的假设检验。从某种意义来说，它是这一问题的推广。

令αi=μi-μ，i=1，2，…，p，称αi为水平Ai的效应，则

xij=μ+αi+εij i=1,2,…,p j=1,2,…,n(www.xing528.com)

显然αi满足。综合以上假定，可建立单因素方差分析模型如下：

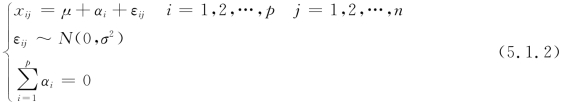
于是检验

H0:μ1=μ2=…=μp

等价于检验

H0:α1=α2=…=αp=0

因此单因素方差分析就是在模型（5.1.2）的假定下，检验假设