独立性检验结果-数理统计学基于R

设二维随机变量（X，Y）的联合分布函数为F（x，y），X和Y的边缘分布函数分别为FX（x）和FY（y）。为检验X和Y的独立性，只需检验

H0：F（x，y）=FX（x）FY（y），对一切x，y成立

H1：F（x，y）≠FX（x）FY（y），存在x，y使式子成立

将X和Y的取值范围分别分成r和k个区间：

A1=(-∞,t1],A2=(t1,t2],…,Ar-1=(tr-2,tr-1],Ar=(tr-1,+∞)

B1=(-∞,s1],B2=(s1,s2],…,Bk-1=(sk-2,sk-1],Bk=(sk-1,+∞)

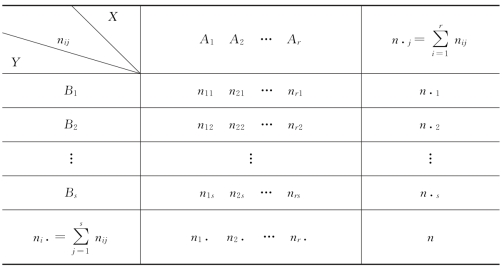
若（X，Y）的样本为（x1，y1），（x2，y2），…，（xn，yn），记nij为X落入Ai、Y落入Bj的样本值的频数。用表格表示如表4.5.2所示（称为r×k列联表）。

表4.5.2　联合频数与边缘频数关系表

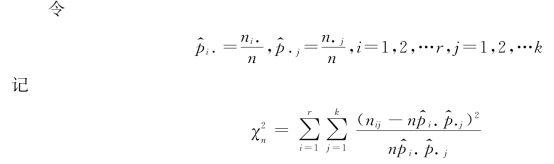
当n→∞时，χ2n～χ2（rk-r-k+1）

由检验水平α，查χ2分布表，得临界值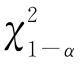（rk-r-k+1），使

由样本值计算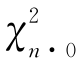的值：

·若，则否定H0；

·若，则不能否定H0。

对于最简单的2×2列联表（如表4.5.3所示）

表4.5.3　2×2列联表

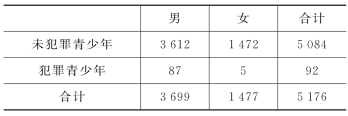
例4.5.3 根据表4.5.4所示调查资料，试研究青少年犯罪是否与性别有关（α=0.01）？

表4.5.4　青少年犯罪调查数据列联表(www.xing528.com)

解 令

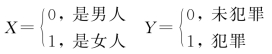
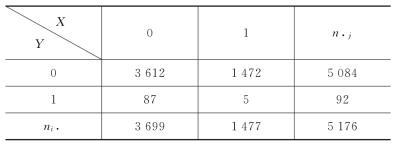
则有表4.5.5。

表4.5.5　符号表示2×2青少年犯罪调查数据列联表

①提出假设：

H0：青少年犯罪与性别无关 H1：青少年犯罪与性别有关

②由检验水平α=0.01，查χ2分布表，得

③计算

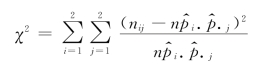
其中

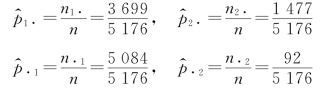
所以

因此否定H0，即青少年犯罪与性别有关。

基于R的求解方法之一如下：

从p值看出，否定原假设，即认为青少年犯罪与性别有关。