基于R的数理统计学:总体分布假设检验结果

在许多问题中，我们不知道总体服从什么类型的分布，这就需要根据样本对总体分布函数F（x）进行假设检验。这种考察理论分布曲线和实际观察曲线相适合程度的检验，常称为拟合适度检验。χ2拟合适度检验（K.Pearson，皮尔逊检验法）是这种检验的常用方法。它是先根据样本和其他信息，对总体分布提出假设H0：总体X的分布函数是F（x），H1：总体X的分布函数不是F（x）。这时，H1通常省略不写。分布函数中的未知参数，可以在H0成立的条件下，用参数估计中的点估计方法先进行估计。

上面提出的假设，在总体X是离散型时，也可以提出如下假设H0：总体X的分布律为P{X=xi}=pi，i=1，2，3，…。在总体X是连续型时，也可以提出如下假设H0：总体X的概率密度函数为f（x）。

现在就分布函数F（x）的假设进行检验，检验方法如下。

①提出假设H0：总体X的分布函数是F（x）。

②在数轴上取k-1个分点：t1＜t2＜…＜tk-1，将数轴分为k个区间：（-∞，t1]，（t1，t2]，（t2，t3]，…，（tk-2，tk-1]，（tk-1，+∞）。

③由假设的分布函数计算概率pi（i=1，2，…，k）的值：

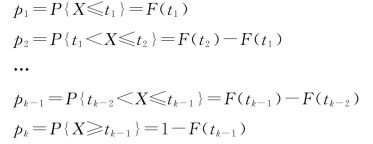
④设样本观察值为x1，x2，…，xn。计算样本值落在第i个小区间的个数fi（i=1，2，…，k）。

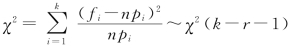⑤在样本容量n较大（一般要求n至少大于50，最好在100以上）和H0成立的条件下，频率与pi应该比较接近。皮尔逊用统计量，其中，r为F（x）中利用样本值求得的极大似然估计的参数个数。

⑥由检验水平α，查χ2分布表，得临界值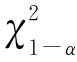（k-r-1），使

⑦由样本值计算，并与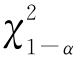（k-r-1）比较：

·若χ2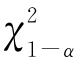＞（k-r-1），则否定H0；

·若χ2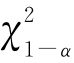＜（k-r-1），则不能否定H0。

在应用χ2检验法时，n要充分大，npi不太小。根据实践，n≥50，npi≥5（i=1，2，…，k）。若npi＜5，则应适当合并区间，使npi≥5。

关于总体分布的检验，随着计算机的快速发展，而采用统计模拟的方法构造出总体的经验分布，由格里汶科定理可知，当样本充分大时，经验分布近似精确分布。

例4.5.1 某厂生产的螺栓中，随机地抽取50个，测得其长度数据（单位：mm）如下：

25.20　35.40 26.00 33.20 31.20 34.00 29.00 24.20 32.80 31.00

29.80　31.60 31.00 34.60 27.40 30.60 37.00 34.60 35.00 16.00

31.00　37.00 32.80 28.80 31.20 38.00 37.40 29.40 35.80 29.80

37.00　34.60 29.40 33.00 29.80 34.80 32.20 30.60 34.00 26.80

33.40　25.00 29.60 29.00 46.00 27.80 33.40 25.00 33.00 36.40

试分析该厂生产的这批产品的长度服从什么分布（α=0.05）？

解 H0：X～N（31.60，4.662） H1：X≁N（31.60，4.662）

由样本值计算，得，用下面六个分点把x轴分成七个区间：t1=24.50，t2=27.00，t3=29.50，t4=32.00，t5=34.50，t6=37.00。七个区间是：（-∞，24.50]，（24.50，27.00]，（27.00，29.50]，（29.50，32.00]，（32.00，34.50]，（34.50，37.00]，（37.00，+∞）。求出样本值落入第i个区间（ti，ti-1]上的频数fi为2，5，7，12，10，11，3。

在H0成立的条件下，计算X落入第i个区间的概率pi：

pi=P{ti-1＜X≤ti}=F(ti)-F(ti-1)(www.xing528.com)

先计算F（ti）：

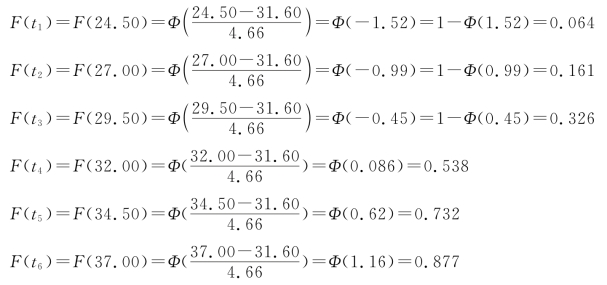
代入计算pi的值：

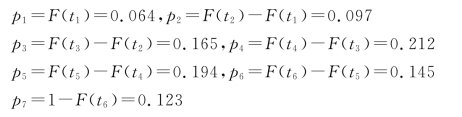
计算结果如表4.5.1所示。

表4.5.1　卡方统计量计算表

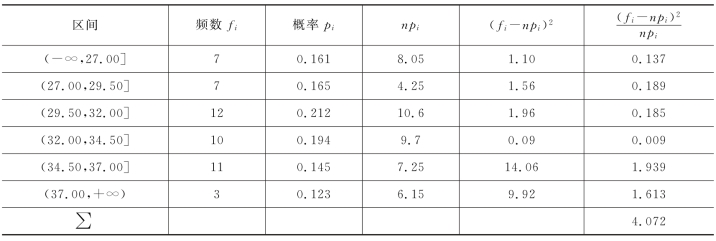
其中，有些npi＜5，前两个区间（-∞，24.50]和（24.50，27.00]需合并为一个区间（-∞，27.00]，使所有npi≥5，经合并后，K=6，r=2，所以，k-r-1=3，由α=0.05，查表得临界值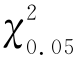（3）=7.815，由样本值计算

所以不能否定H0，即认为这批产品的长度服从正态分布N（31.60，4.662）。

对于连续型随机变量，用χ2检验法计算量很大。但是，对于离散型随机变量，计算量要小得多，使用起来较方便。

基于R的求解方法之一如下：

从p值看，不能否认来自正态分布，均值方差由x的样本均值和方差确定。

例4.5.2 掷一枚硬币100次，“正面”出现了40次，问这枚硬币是否匀称（α=0.05）？

解 如果硬币是匀称的，则“正面”出现的概率应为1/2。记X=1表示“正面”出现，X=0表示“反面”出现。

H0:P{X=1}=P{X=0}=1/2

用一个分点0.5把数轴分为两部分：（-∞，0.5]，（0.5，+∞）。

p1=P{X≤0.5}=P{X=0},p2=P{X＞0.5}=P{X=1}

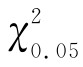如果H0成立，则p1=p2=1/2，且由检验水平α，查表得临界值（1）=3.84，np1=50，np2=50，f1=60，f2=40，得

所以否定H0，即认为这枚硬币不是匀称的。

基于R的求解方法之一如下：

从p值可以看出，拒绝原假设，即认为硬币是不均匀的。