基于R的数理统计学：两个正态总体假设检验

设总体X～N（μ1，σ21），Y～N（μ2，σ22），且X和Y独立，（X1，X2，…，Xn1）和（Y1，Y2，…，Yn2）分别是来自总体X和Y的样本。关于两个正态总体的假设检验，主要有下面几种类型。

1.均值（或均值差）的检验

（1）已知方差σ21和σ22，检验H0：μ1=μ2，H1：μ1≠μ2。

在H0成立的条件下，

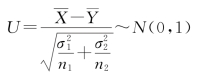
由检验水平α，查标准正态分布表，得临界值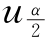，使，即是小概率事件，

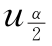由样本值计算，并与比较：

·若，则否定H0；

·若，则不能否定H0。

（2）未知σ21和σ22，但已知σ21=σ22，检验H0：μ1=μ2，H1：μ1≠μ2。

这种类型的检验步骤与类型（1）相似。但必须选用下面的统计量：

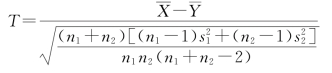
其中，

且在H0成立的条件下，T～t（n1+n2-2）。

（3）未知σ21和σ22，且σ21≠σ22，但n1=n2=n，检验H0：μ1=μ2，H1：μ1≠μ2。

通常采用配对试验的t检验法，其做法如下。

令

Zi=Xi-Yi,i=1,2,…,n

则

Zi～N(μ1-μ2,σ21+σ22)

视（Z1，Z2，…，Zn）为总体Z～N（μ1-μ2，σ21+σ22）的一个样本，于是所要进行的检验等价于一个正态总体，方差未知，检验

H0:μ1-μ2=0,H1:μ1-μ2≠0

记

则在H0成立的条件下，选用统计量

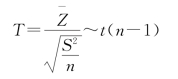
即可。

这种检验通常应用于用两种产品、两种仪器、两种方法得到成对数据，需要比较其质量或效果好坏的情况。

（4）未知σ21和σ22，且σ21≠σ22，n1≠n2（n1＜n2），检验H0：μ1=μ2，H1：μ1≠μ2。

令

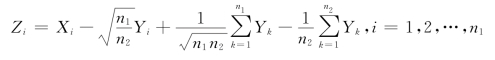
则

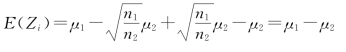
其中，

Cov(Zi,Zj)=0(i≠j,i,j=1,2,…,n1)

于是，视（Z1，Z2，…，Zn1）为来自正态总体的一个样本。原来的问题等价于一个正态总体，未知方差，检验H0：μ1-μ2=0，H1：μ1-μ2≠0。

在H0成立的条件下，选用统计量

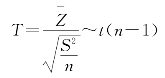(www.xing528.com)

即可，其中

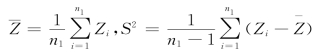
2.方差（或方差比）的检验

未知均值μ1和μ2，检验H0：σ21=σ22，H1：σ21≠σ22。

在H0成立的条件下，

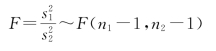
由检验水平α，查F分布表，得临界值

使

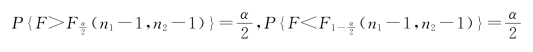
即

是小概率事件。由样本值计算F0，并与临界值进行比较：

·若F0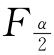＞（n1-1，n2-1），或F0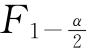＜（n1-1，n2-1），则否定H0；

·若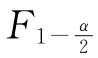（n1-1，n2-1）＜F0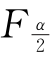＜（n1-1，n2-1），则不能否定H0，称

为否定域。

例4.3.1 甲、乙两台机床，生产同一型号的滚珠，由以往经验可知，两台机床生产的滚珠直径都服从正态分布，现从这两台机床生产的滚珠中分别抽出5个和4个，测得其直径（单位：mm）如下：

甲机床：24.3 20.8 23.7 21.3 17.4

乙机床：14.2 16.9 20.2 16.7问：甲、乙两台机床生产的滚珠直径的方差有无显著差异（α=0.05）？

解 H0：σ21=σ22 H1：σ21≠σ2

2

在H0成立的条件下，

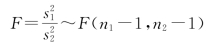
由检验水平α，查F分布表，得临界值

F0.975(4,3)=15.10

和

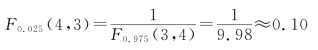
由样本值计算

因为0.10＜F0＜15.10，所以不能否定H0，即认为方差无显著差异。

基于R的求解方法之一如下：

从p值可以看出不能否认原假设。

·对于单侧检验H0：σ21≥σ22，H1：σ12＜σ22，其否定域为（0，F1-α（n1-1，n2-1））；

·对于单侧检验H0：σ21≤σ22，H1：σ21＞σ22，其否定域为（Fα（n1-1，n2-1），+∞）。

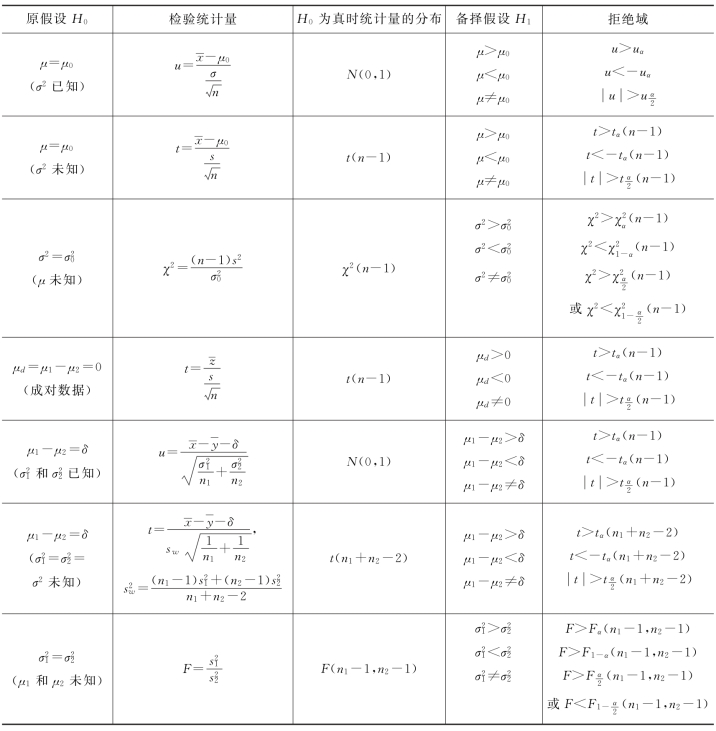
通常遇到的参数假设检验的各种类型及否定域如表4.3.1所示。

表4.3.1　正态总体均值、方差的检验法（显著性水平为α）