基于R的数理统计学：假设检验基本概念

上一章介绍了统计推断的一类重要问题——参数估计。它是由样本求出总体参数的估计值，或者参数的取值范围。本章将要介绍统计推断的另一类重要问题——假设检验。它是由样本来推断有关总体分布或分布参数的某一假设是否成立。例如一台自动包糖机，规定由它包装的每包糖的标准重量是500 g。每天开工后，需要检验包糖机工作是否正常，为此必须检查糖包的重量是否符合标准。如果从生产线上抽取一个样本，得到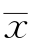-500=0.012 g，产生这样的误差是包糖机出现系统误差还是随机因素所致？用假设检验方法可以回答这一问题。假设检验的过程是：首先可以提出假设“包糖机没有系统误差”，然后根据生产线上抽取的样本，来判断这个假设是否与事实相符，从而做出否定或不否定“包糖机没有系统误差”这一假设。

在概率论中，“小概率事件在一次试验中是几乎不可能发生的”，称为小概率事件原理。因此，如果在某种假设下得出的小概率事件，在一次试验中竟然发生了，这是不合理的，由此否定该假设，这是假设检验的基本原则。

假设检验的基本思想是概率意义下的反证法。例如，设鱼塘里有两种鱼：草鱼和胖头鱼，已知两种鱼的比例是9∶1，但不知哪种鱼较多。为了弄清这个问题，可以先提出一个假设：“草鱼数比胖头鱼数是9∶1（即草鱼比胖头鱼多）”。如果这一假设成立，便可以断言：“从鱼塘中随机地捕捞15条鱼，胖头鱼比草鱼多”是一个小概率事件。如果我们实际捕捞15条鱼，这个小概率事件竟然发生了，这是不合理的。由此可推断“草鱼数比胖头鱼数是9∶1”的假设应予以否定。如果这个小概率事件不发生，则我们不能否定这个假设。这就是假设检验的基本思想。

假设检验中提出的待检验假设，称为原假设（或零假设），用H0表示。如果H0被否定，就意味着另一个对立的假设H1不能被否定，称H1为备择假设。(www.xing528.com)

假设检验中所指的小概率事件，到底概率多小才算小概率，通常是事先给定α=0.05、α=0.01或根据实际问题的需要而确定的一个较小的正数。它表示在假设检验中，概率小于α的事件被认为是小概率事件，称α为显著性水平或检验水平。

假设检验中主要研究两类问题的检验：一类是总体分布形式已知，仅需对总体未知参数进行检验，称为参数假设检验；另一类是总体分布形式所知甚少，而要假设其具体形式的假设检验，称为非参数假设检验。