大样本情况下总体均值的区间估计

设总体X的分布是任意的，均值μ=E（X）和方差σ2=D（X）都是未知的。用样本（X1，X2，…，Xn）对总体平均数μ作区间估计。

由概率论中的中心极限定理可知，不论所考察的总体分布如何，只要样本容量n足够大，样本均值近似地服从正态分布。又，所以近似地服从标准正态分布N（0，1）。然而，在n很大时，σ可用样本标准差S近似，且上式中σ换成S后对它的分布影响不大，故当n很大时，

仍近似地服从标准正态分布。给定1-α，可找到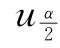，使

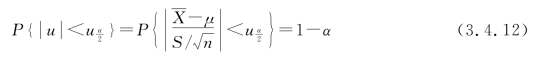
于是μ的置信区间是

而置信度（近似）等于1-α，需要指出，用式（3.4.13）求置信区间对n很大的样本适用，这是由于导出u的近似分布用到了中心极限定理。n多大的样本可以认为是大样本呢？严格来讲，这取决于u的分布收敛到标准正态分布的速度，而收敛速度又与总体分布有关。中心极限定理没有对这个问题作出解释。实际经验一般认为n≥50的样本是大样本。

例3.4.8 某市为了解在该市民工的生活状况，从中随机抽取了100个民工进行调查，得到民工月平均工资为3 300元，标准差为60元，试在95%的概率保证下，对该市民工的月平均工资作区间估计。

解 按题意n=100，可以认为是大样本。已知1-α=95%，查附表2得=1.96，由式（3.4.13）有置信下限

置信上限

故置信度95%的置信区间为（3 288.24，3 311.76）。

下面考察总体X服从二点分布B（1，p）的情形，其分布律为P｛X=1｝=p，P｛X=0｝=1-p，从总体中抽取一个容量为n的样本，其中恰有m个“1”，现对p作区间估计。此时，(www.xing528.com)

在最后一式推导中，需注意Xi仅能取“1”和“0”，把这些量代入式（3.4.12），得p的置信区间是

而置信度为1-α。

例3.4.9 从一大批产品中随机地抽出100个进行检测，其中有4个次品，试以95%的概率估计这批产品的次品率。

解 记次品为“1”，正品为“0”，次品率为p。总体分布是二点分布B（1，p），根据题意，n=100，m=4，由1-α=0.95得=1.96。利用式（3.4.14）得置信下限

置信上限

故置信区间是（0.002，0.078）。

需要指出，上面介绍的两种情况均属于总体分布为非正态分布的情形，如果样本容量较大（一般n≥50），可以按正态分布来近似其未知参数的估计区间。如果样本容量较小（一般n＜50），不能用上述的方法求参数的估计区间。

参数估计采用表格的形式小结于表3.4.1中。

表3.4.1　均值μ和方差σ2的双侧置信区间