5炉铁水含碳量的95%置信区间估计

什么叫作参数区间估计？如前所述，参数的点估计（定值估计）是由样本求出未知参数的一个估计值，而区间估计则要由样本给出参数值的一个估计范围。例如，某批产品的不合格率估计在1%到3%之间，某物体长度估计在10.6 mm到11.0 mm范围之间，等等。由于数理统计中未知参数所在范围是依据一个样本作出来的，没有百分之百的把握，只能对一定可靠程度（概率）而言，例如以95%的概率估计未知参数θ在1.2到1.5之间。因此，参数的区间估计就是由样本给出参数的估计范围，并使未知参数在这个范围中具有指定的概率。下面通过实例具体介绍区间估计的方法。

例3.3.1 已知某炼铁厂的铁水含碳量（%）在正常情况下服从正态分布，且标准差σ=0.108。现测量五炉铁水，其含碳量分别是4.28，4.40，4.42，4.35，4.37，试以概率95%对总体均值μ作区间估计。

首先建立此例的数学模型。设总体X的分布是N（μ，σ02），σ0已知，从总体中随机地抽得样本（X1，X2，…，Xn），要求以概率1-α（0＜α＜1）对总体均值μ作区间估计。

记总体分布为N（μ，σ20）。考察样本X1，X2，…，Xn，自然可用样本均值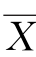估计μ，由抽样分布定理知服从正态分布，因而

对于给定概率1-α（0＜α＜1），则存在uα/2使

从图3.3.1容易看出，uα/2是标准正态分布的上分位数，它的数值可以用R或Excel计算或查表得到。

图3.3.1　标准正态分布的双侧分位数图

把u的表示式（3.3.1）代入式（3.3.2）得

即

可改写为

故μ的1-α置信区间为

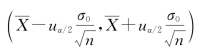
和分别称为μ的置信下限和置信上限。1-α称为置信概率或置信度，工业上通常取1-α的数值为90%、95%或99%。

在例3.3.1中，σ0=0.108，n=5，由样本数值算得样本均值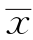=4.364，由1-α=0.95，R计算得uα/2=1.96，把这些数值代入式（3.3.3）得(www.xing528.com)

即μ的置信区间是（4.269，4.459），置信度为0.95。

基于R的求解方法一：

基于R的求解方法二：

注：两种做法结果相同。

怎样理解μ的置信度为95%的置信区间为（4.269，4.459）呢？这个结果是由式（3.3.3）得到的，式（3.3.3）说明随机区间覆盖μ的可能性是95%（1-α=0.95），亦即反复抽容量为100的样本算得μ的置信区间，平均有95个置信区间包含真正的参数μ。因而，对于一次抽样后由样本算得的置信区间，我们可以认为该置信区间是这些区间中的一个。置信区间的长短刻画估计参数的精确程度，人们习惯用置信区间长度的一半作为估计的精度。置信度表示未知参数落在置信区间中的可靠程度。

由式（3.3.3）可见置信区间的中心是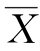，置信区间的长度等于如果在式（3.3.2）中u的取值改为关于原点不对称的区间，即取u1和u2使P{u1＜u＜u2}=1-α，利用式（3.3.1）可得

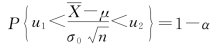
这样获得μ的置信区间的中心不是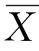。可以证明u2-u1＞2uα/2，所以此法得到的置信区间长度u2-u1大于用前面方法得到的置信区间长度，这说明用前面方法所得到的置信区间在众多置信区间中是最小的，因此估计的精确度最高，故前一方法较为合理。

哪些因素影响置信区间长度呢？当n一定时，如果置信度1-α愈大，则uα/2愈大，故置信区间愈长。

对于一定容量的样本，要估计的可靠程度愈高，估计的范围当然愈大；反过来，要求估计范围小就要冒一定风险。当α一定时，n愈大，置信区间愈短，这与直观也一致，取样越多，估计当然愈精确。

求出置信区间的方法是：首先确定待估参数μ，再求出未知参数μ的估计量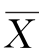，由未知参数μ和估计量作出函数u，它的分布是已知的，且与未知参数μ无关；然后根据给定的置信度与函数u的分布推导出置信区间，这种方法具有一定的普遍性。

一般的，设总体X的分布函数是F（x；θ），其中θ是未知参数。从总体中抽取样本（X1，X2，…，Xn），作统计量θ1（X1，X2，…，Xn）和θ2（X1，X2，…，Xn），使

P{θ1＜θ＜θ2}=1-a

其中（θ1，θ2）称为θ的置信区间，θ1和θ2分别称为置信下限和置信上限，1-α称为置信度。

下面分各种情况对总体平均数和方差作区间估计。