基于R的数理统计学-点估计方法

1.矩估计法

所谓矩估计法，概括来说，就是用样本矩估计总体的相应的矩，用样本矩的函数作为总体相应矩同一函数的估计量。

例3.1.2 设某种罐头的重量X～N（μ，σ2），其中参数μ及σ2都是未知的，现随机地抽测8盒罐头，测得重量（单位：g）为

453 457 454 452.5 453.5 455 456 451

试求μ及σ2的矩估计值。

解 因为μ是全部罐头的平均重量，而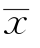是样本的平均重量，因此自然会想到用样本均值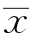去估计μ。同样，用样本方差s2去估计总体方差σ2，即有，由测得重量值可算得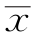和s2的值分别是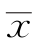=454，s2=3.78，故有

基于R的求解过程如下：

例3.1.3 设总体X在[a，b]上是均匀分布的，其概率密度函数为

试求未知参数a和b的估计量。

解 这时参数a和b并不是总体分布的矩，但是总体矩却都与a和b有关，例如总体分布的一阶、二阶原点矩分别为

由上面二式可解得

当我们用样本矩估计总体矩，即取时，就得到

例3.1.4 设总体X服从参数λ的指数分布，求λ的矩估计量。

解 由题意得：f（x）=λe-λx（x＞0，λ＞0），则

即

设X1，X2，…，Xn是来自总体X的样本，A1的估计量为

故

一般来讲，设总体X的分布函数F（x；θ1，θ2，…，θm）的类型已知，但其中包含m个未知参数θ1，θ2，…，θm，则总体X的k阶矩也是θ1，θ2，…，θm的函数，记

qk(θ1,θ2,…,θm)=E(Xk),k=1,2,…,m

假定从方程组

可以解出

设X1，X2，…，Xn是总体X的一个样本。用来估计Ak，其中k=1，2，…，m，然后代入上式的hk中，得到θk的估计量，其中k=1，2，3，…，m。

我们看到，矩估计法直观而又便于计算，特别是在对总体的数学期望及方差等数字特征作估计时，并不一定要知道总体的分布函数，但是矩估计法要求总体X的原点矩存在，若总体X的原点矩不存在，那就不能用矩估计法。

2.最大似然估计法

当总体的分布类型已知时，常用最大似然估计法估计未知参数。下面结合例子介绍最大似然估计法的基本思想和方法。

例3.1.5 设有一大批产品，其不合格率为p（0＜p＜1）。现从中随机地抽取100个，其中有10个不合格品，试估计p的值。

解 若正品用“0”表示，不合格品用“1”表示。此总体X的分布为

P{X=1}=p,P{X=0}=1-p

即

P{X=x}=px(1-p)1-x,x=0,1

取得的样本记为（x1，x2，…，x100），其中10个是“1”，90个是“0”。出现此样本的概率为

这个概率随p不同而变。自然应该选择使此概率达到最大的p的值作为真正不合格率的估计值。记L（p）=p10（1-p）90。用高等数学中求极值的方法，知

解得

此例求解的方法是：选择参数p的值使抽得的该样本值出现的可能性最大，用这个值作为未知参数p的估计值。这种求估计量的方法称为最大似然估计法，也称为极大似然估计法。显然，在上例中取一个容量为n的样本，其中有m个不合格品，用最大似然估计法可得

下面分离散和连续两种总体分布情形介绍最大似然估计法。

（1）离散分布情形

设总体X的分布律为P{X=xi}=p（xi；θ），i=1，2，…。其中θ为未知参数，（X1，X2，…，Xn）为X的一个样本，（x1，x2，…，xn）是样本的观察值。则

当样本观测值（x1，x2，…，xn）给定后，它是θ的函数，记作

并称它为似然函数。使似然函数L取得最大值的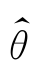，即满足

的，称为θ的最大似然估计值。

怎样求θ的最大似然估计值呢？当L是θ的可微函数时，要使L取得最大值，则θ必须满足方程

从此方程解得θ，再把θ换成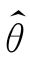即可。

由于L与ln L在同一处取得最大值，所以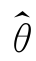可由方程

求得。这往往比直接用式（3.1.2）求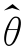来得方便。式（3.1.2）称为似然方程；式（3.1.3）称为对数似然方程。显然，用最大似然估计法得到的参数θ的估计值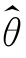与样本观测值（x1，x2，…，xn）的取值有关，故可记作称为θ的最大似然估计量。

综上所述，求参数θ的最大似然估计的步骤归纳如下：

第一步，根据总体概率分布（若是连续型变量，则根据概率密度）构造似然函数：L（xi；θ）=

第二步，对似然函数取对数；

第三步，对数似然函数ln L对θ求导数（若同时估计总体的m个未知参数θi（i=1，2，…，m），则对数似然函数ln L分别对θi求偏导数），并令

第四步，从上式中解出θ，由于θ是样本的函数，所以是θ的估计量，记为；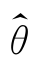

第五步，将样本观测值代入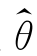，得到总体参数θ的估计值。

例3.1.6 设总体X服从泊松分布，其分布律为（X1，X2，…，Xn）是X的一个样本，试求λ的最大似然估计量。(www.xing528.com)

解 按式（3.1.1），似然函数为

取对数得

对λ求导得对数似然方程

由此得λ的最大似然估计值为

λ的最大似然估计量为

（2）连续分布情形

设总体X的分布密度为f（x；θ），θ为未知参数，（x1，x2，…，xn）为X的一个样本观测值，以f（xi；θ）代替式（3.1.1）中的p（xi；θ），得似然函数

再按（1）离散分布情形中的方法和步骤便可求得θ的最大似然估计值及最大似然估计量。

需要指出，似然函数与联合概率密度函数的区别在于，在式（3.1.4）中，若θ是已知的，则为联合概率密度函数；若θ是未知的，则为似然函数。

例3.1.7 设某种电子元件的寿命服从指数分布，其分布密度为

今测得n个元件的寿命为x1，x2，…，xn，试求λ的最大似然估计值。

解 按式（3.1.4），似然函数为

取对数得

对λ求导得对数似然方程

由此解得λ的最大似然估计值

例3.1.8 设总体X具有均匀分布，其密度为

其中，未知参数θ＞0，试求θ的极大似然估计量。

解 样本值为（x1，x2，…，xn），而

似然函数

选取θ的值使L达到最大，只要取

改写成

一般来说，设总体X的分布中含有m个未知参数θ1，θ2，…，θm，其似然函数为

L=L(x1,x2,…,xn;θ1,θ2,…,θm)

则似然方程组为

对数似然方程组为

由式（3.1.5）或式（3.1.6）解得的分别称为参数θ1，θ2，…，θm的最大似然估计量。

例3.1.9 设正态总体X具有分布N（μ，σ2），其中μ和σ2是未知参数，试求μ和σ2的最大似然估计量。

解 因为

似然函数为

取对数得

求导得对数似然方程组为

解方程组得

改写为

需要指出，最大似然估计法不仅利用了样本所提供的信息，同时也利用了总体分布的表达式所提供的关于参数θ1，θ2，…，θm的信息。因此最大似然估计法得到的估计量的精度一般比矩估计法高，而且它的适用范围也比较广，到目前为止，在理论上它仍是参数点估计的一种最重要的方法。

3.顺序统计量法

实际上，常用的顺序统计量是样本中位数和样本极差。顺序统计量法直观地来讲就是用样本中位数Me估计总体中位数，用样本极差R估计总体标准差。在总体为连续型且分布密度为对称的情形，总体中位数也就是期望值。特别对正态总体N（μ，σ2），关于样本中位数的下面结果能使我们更好地认识这种估计法。

定理 设（X1，X2，…，Xn）是来自正态总体N（μ，σ2）的样本，Me是样本中位数，则有

证明略。

此定理表明：渐近标准正态分布N（0，1），从而当n充分大时，Me近似服从，n越大，Me落在μ的附近的概率就越大。所以，当n充分大时，可用样本中位数Me作为均值μ的估计，即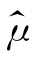=Me。

例3.1.10 设某种灯泡寿命X～N（μ，σ2），其中参数μ和σ2未知，为了估计平均寿命μ，随机抽取7只灯泡测得寿命（单位：h）为

1575 1503 1346 1630 1575 1453 1950

（1）用顺序统计量法估计μ；

（2）用矩估计法及最大似然估计法估计μ。

解 （1）顺序统计量（X（1），X（2），…，X（n））的观测值分别为1346，1453，1503，1575，1575，1630，1950。因为n=7，所以

（2）当总体X～N（μ，σ2）时，用矩估计法及最大似然法去估计μ都得

当总体均值μ能够用样本中位数Me估计时，用Me估计有以下优点：只要E（X）存在而不需要利用总体X的分布；计算简便；样本中位数Me的观测值不易受个别异常数据的影响。

例如，在寿命试验的样本值中，发现某一数据异常小（譬如，在例3.1.10中，由于粗心，把数据1 346误记录为134），在进行统计推断时一定会提疑问：这个异常小的数据是总体X的随机性造成的，还是受外来干扰造成的呢？如果原因属于后者（如记录错误），那么用样本均值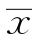估计E（X）显然就要受到影响，但用样本中位数Me估计E（X）时，由于一个（甚至几个）异常数据不易改变中位数Me的取值，所以估计值不易受影响。特别在寿命试验中，个别样本寿命很长，这是常有的现象，若等待n个寿命试验全部结束，然后计算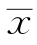作为平均寿命的估计值，花的时间就较多；如果用Me估计总体均值E（X），那么将n个试验同时进行，只要有超过半数的试验得到了寿命数据，无论其余试验结果如何，都可得到样本中位数的观测值Me，因此得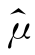=Me，若没有别的需求，寿命试验即可结束。

类似的，可用极差R=x（n）-x（1）作为总体标准差的估计量，即

这种估计称为极差估计法。

用样本极差R来估计，计算很简单，但不如用S来得可靠。一般情况下，这种估计仅在n≤10时使用。