基于R的数理统计学-参数估计方法

参数估计的参数是指总体分布中的未知参数。例如，在正态分布N（μ，σ2）中μ与σ2未知，μ与σ2是参数；再如，泊松分布π（λ）的总体中λ未知，λ是参数；二项分布B（n，p）的总体中n已知，p未知，p是参数。所谓参数估计就是由样本值对总体的未知参数作出估计。先看一个实例。

例3.1.1 用一个仪器测量某物体的长度，假定测量得到的长度服从正态分布N（μ，σ2）。现在进行五次测量，测量值（单位：mm）为：53.2，52.9，53.3，52.8，52.5，μ和σ2分别是正态分布总体的均值和方差。很显然，可以用样本均值和样本方差分别去估计。

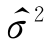所以，μ的估计值是52.94，σ2的估计值是0.103。用和分别表示μ和σ2的估计值，故=52.94=0.103，这就是对参数μ和σ2分别作定值估计，亦称为参数的点估计。

基于R求解本例如下：(www.xing528.com)

一般来说，设总体X的分布函数是F（x；θ1，θ2，…，θk），其中θ1，θ2，…，θk是未知参数。如果从总体中取得的样本值为（x1，x2，…，xn），作k个函数2，…，k，分别用估计未知参数θi，则称是θi的估计值。作，则称（随机变量）是θi的估计量，i=1，2，…，k。估计量显然是统计量，用作估计未知参数。为了方便起见，有时候我们把估计值和估计量统称为估计量，这种用对参数θi作定值估计的方法，称为参数的点估计。需要指出，这种估计值随抽得的样本的数值不同而不同，具有随机性。

下面介绍参数点估计的几个具体方法。