【摘要】:定义2.3.1 设X1,X2,…,Xn是来自总体N(0,1)的样本,则称统计量服从自由度为n的χ2分布,记为χ2~χ2。可以证明:χ2分布的概率密度函数为其中,,称为Gamma函数。f的图形如图2.3.1所示。图2.3.1自由度不同的卡方密度曲线χ2分布具备如下一些性质。图2.3.2卡方分布的100α%分位数χ2α从定义可以看出:因此,可利用χ2分布的分位数值表求得χ2随机变量落在任何一个区间内的概率。
定义2.3.1 设X1,X2,…,Xn是来自总体N(0,1)的样本,则称统计量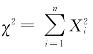 服从自由度为n的χ2分布,记为χ2~χ2(n)。
服从自由度为n的χ2分布,记为χ2~χ2(n)。
可以证明:χ2(n)分布的概率密度函数为
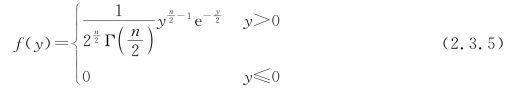
其中,![]() ,称为Gamma函数。
,称为Gamma函数。
f(y)的图形如图2.3.1所示。
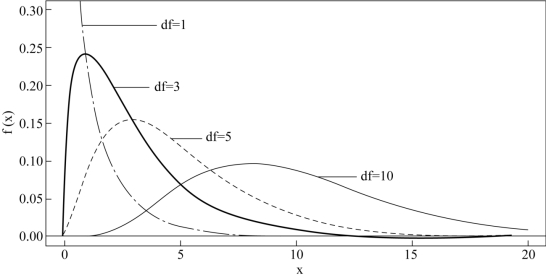
图2.3.1 自由度不同的卡方密度曲线(基于R绘制)
χ2分布具备如下一些性质。
(1)若![]() ,且
,且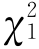 与
与 相互独立,则
相互独立,则
![]()
(2)若χ2~χ2(n),则
E(χ2)=n,D(χ2)=2n
我们仅就第2个性质说明如下。
因为Xi~N(0,1),所以
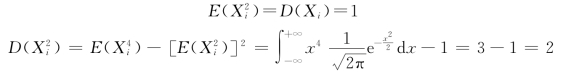 (https://www.xing528.com)
(https://www.xing528.com)
于是
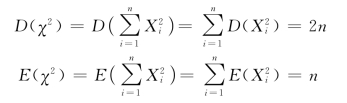
当X1,X2,…,Xn是来自总体N(μ,σ2)的样本时,也记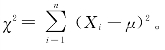
事实上,令
![]()
显然,Y1,Y2,…,Yn相互独立,且服从同一分布N(0,1),所以由定义2.3.1知:
![]()
关于χ2分布,人们引入了分位数(Fractile)(也称分位点、临界值或阈值)的概念,并制成了相应的分位数值表(见附表4),可供查询。
定义2.3.2 对任意正数α,0<α<1,若P{χ2>χ2α(n)}=α,则称χ2α(n)为χ2分布的100α%分位数,如图2.3.2所示。
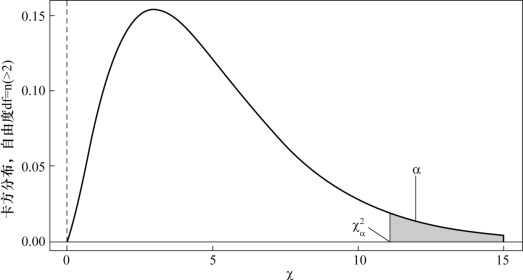
图2.3.2 卡方分布的100α%分位数χ2α(n)(基于R绘制)
从定义可以看出:
![]()
因此,可利用χ2分布的分位数值表求得χ2随机变量落在任何一个区间内的概率。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




