在数理统计中,直观地可将研究对象的全体称为总体(Population),而把组成总体的每个元素称为个体。通过对一部分个体信息的观察来估计、推断总体的某些信息,正是数理统计所要研究的课题。在这里,我们关于对象的研究不是泛泛的,而是常常要具体到研究对象的一项或几项数量指标值,比如灯泡的寿命、人的身高和体重、股票的当日收盘价格等。在这个意义上,研究对象的全体实际上体现为研究对象的某项数量指标值的全体。又由于这些数值可能有重复,如灯泡的寿命,可能有许多灯泡的寿命是5 000小时,而只有一只的寿命是10 000小时,这就是说,这些数量指标的每个值所占的比重不一样,即每个数值在这些数据中出现的概率不一样。这样总体就对应了一个具有一定概率分布的随机变量。因此在数理统计问题的研究中,所谓总体就是相应其取值分布的随机变量,如图2.2.1所示。
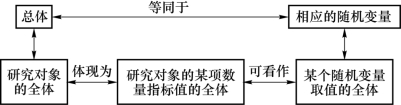
图2.2.1 总体与相应随机变量对应图
由于总体的取值在客观上具有一定的分布,因此相应随机变量的分布和数字特征就是总体的分布和数字特征,而关于总体的研究实际上就是对相应随机变量X的分布的研究。所以,有时在讨论中总体、随机变量、分布这三者不加区分。
那么,为什么不能对每一个个体进行试验或观察,从而“精确”掌握研究对象的整体情况,而只能按照所谓数理统计的方式通过部分来推断整体呢?归纳起来有如下几个方面的原因。
(1)检验全部对象有时是不可能的。如对某些产品的质量检验是破坏性的,像灯泡的寿命检验、钢丝拉力强度的检验、电视机显像管无故障工作时间的检验等都是如此。如果我们对所有产品进行这种破坏性检验,就没有产品可供销售了。再如,研究某区域海水中微生物的繁殖情况,我们无法将全部海水装进试管里进行检验;在石油勘探中,人们只能选取有限个点进行试钻,绝不可能将所有可能储油的区域钻得遍地窟窿,等等。
(2)对全部对象进行检验需要的成本很高,或所需的时间很长,或两者兼而有之。例如,人口普查:自新中国成立以来,我国共进行了6次全国性的人口普查,进行一次普查需要花费大量的人力物力,而取得的全部数据也需要相当长的时间甚至几年才能处理完毕,因此我们不可能每年都进行人口普查,对大多数年份只能进行抽样调查。城镇居民收入与消费结构调查:由于所涉及的内容更加广泛,对全体城镇居民进行这类调查的费用和工作量可能比人口普查还要大几十倍,但我们从各种媒体中却常常可以看到此类年度、季度甚至是月度数据,可见这些数据只能来自抽样调查,等等。
(3)虽然通过部分信息来推断整体的情况必定会带来误差,但在许多情况下,这种误差是可以容忍的。因为并不是所有问题都需要一个精确的估量,也不是所有问题都能够得到一个非常精确的估量(即使对所有对象进行调查),何况任何统计数据都需要有一个明确的计量单位,在不同的计量单位下,“精确”与“不精确”本身就是可以转换的。例如,在全国性人口普查中,我们不可能也没有必要将统计数据精确到“个”,通常精确到“万”“十万”甚至“百万”即可;在消费者意愿调查中,我们知道每个个人的“意愿”都是可以改变的,即使我们对全体消费者进行了调查,但是“精确”的调查却得到“不精确”的结果,无疑是得不偿失的。
因此,一般说来,对于相当多的实际问题,我们总是从总体中抽取一部分个体进行观察,然后依据所得数据来推断总体的性质。这样被抽出的部分个体称为来自总体的一个样本(Sample),就是说,在相同的条件下对总体X进行了n次独立重复的观察(即进行了n次独立重复的试验),并记录到n个观察结果,通常总是按照试验的次序把这个样本记为:X1,X2,…,Xn(它们是n个随机变量)。这n次观察一经完成,我们便得到一组具体的实数:x1,x2,…,xn,它们依次是X1,X2,…,Xn的观察值,称为样本值(Sample Value)。统计推断就是根据这些数据来判断总体的。
抽取样本的目的是为了对总体的分布规律进行各种分析和推断,因而要求抽取的样本要能够很好地反映总体的特性和变化规律,这就必须对随机抽样的方法提出一定的要求。通常提出以下两点:(https://www.xing528.com)
(1)代表性:即要求样本的每个分量Xi与所考察的总体具有相同的分布F(x);
(2)独立性:即要求X1,X2,…,Xn为相互独立的随机变量,也就是说,每个观察结果既不影响其他结果,也不受其他观察结果的影响。
满足以上两点性质的样本X1,X2,…,Xn称为简单随机样本(Simple Random Sample),获得简单随机样本的方法或过程称为简单随机抽样(Simple Random Sampling)。在本书中,我们所讨论的样本都是指简单随机样本。
定义2.2.1 设X的分布函数为F(x),若X1,X2,…,Xn是具有同一分布函数F(x)的、相互独立的随机变量,则称X1,X2,…,Xn为从分布函数F(X)(或总体X)得到的容量为n的简单随机样本,简称样本,它的观察值x1,x2,…,xn称为样本值,又称为X的n个独立的观察值。
于是,X1,X2,…,Xn的联合分布函数为
![]()
在连续型情形下,X1,X2,…,Xn的联合概率密度函数为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




