求幂级数收敛域与和函数

例7.28（南京大学1996年竞赛题）　求幂级数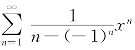的收敛域.

解析　令，则收敛域半径

当x＝1时原幂级数为，而发散，即x＝1时原级数发散.

当x＝－1时，原幂级数为

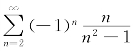令，所以f（x）严格减，因此f（n）也严格减，又，据莱布尼兹判别法得收敛；又因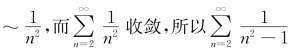收敛.于是x＝－1时原级数收敛.

故?所求收敛域为［－1，1）.

例7.29（北京市1996年竞赛题）　求级数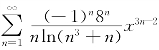的收敛域.

解析　令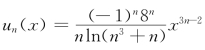，由于

故当时，原级数收敛.

当原级数化为，为莱布尼兹型级数，故收敛.

当，原级数化为，因为

而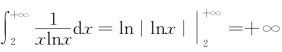，应用积分判别法可得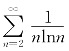发散.因此由比较判别法得级数发散，因而发散.

综上所述，收敛域为

例7.30（江苏省2004年竞赛题）　求幂级数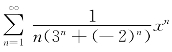的收敛域.

解析　令，则

所以幂级数的收敛半径R＝3.当x＝3时，原幂级数化为.因为发散，由比较判别法知x＝3时原幂级数发散.当x＝－3时，原级数化为

因为为莱布尼兹型级数，收敛；令，由于bn＞0，且

由比值判别法知收敛，故x＝－3时原幂级数收敛.故所求收敛域为［－3，3）.

例7.31（江苏省2002年竞赛题）　求幂级数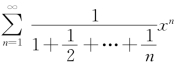的收敛域.

解析　令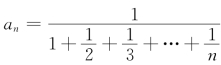，因级数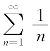发散，故部分和，由于n→∞时

所以收敛半径R＝1.当x＝1时，原级数为，由于

应用比较判别法得发散.当x＝－1时，原级数为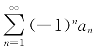，因an→0，且数列｛an｝单调减，应用莱布尼兹判别法得收敛.所以原幂级数的收敛域为［－1，1）.

例7.32（北京市1994年竞赛题）　求级数的收敛半径及和函数.

解析　令，则n≥1时均有1≤an≤n，而1，由夹逼准则可知，所以幂级数的收敛半径R＝1.

令

易知级数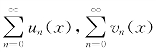在（－1，1）上绝对收敛，应用绝对收敛级数的乘法规则，有

故幂级数的和函数为

例7.33（江苏省2006年竞赛题）　（1）设幂级数的收敛域为［－1，1］，求证：幂级数的收敛域也为［－1，1］.

（2）试问命题（1）的逆命题是否正确？若正确，给出证明；若不正确，举一反例说明.

解析　（1）因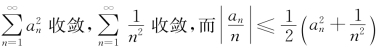，由比较判别法得在x＝±1时（绝对）收敛.下面证明：∀x0，｜x0｜＞1，级数发散.（反证法）设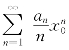收敛，则对∀r，只要｜r｜＜｜x0｜，则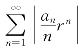收敛，取r1使得1＜｜r1｜＜｜r｜＜｜x0｜.因，所以n充分大时，.于是

故收敛，此与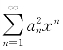在｜x｜＞1时发散矛盾.所以幂级数的收敛域为［－1，1］.

（2）命题（1）的逆命题不成立.反例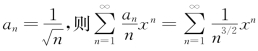，其收敛域为［－1，1］，但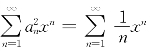的收敛域为［－1，1）.

例7.34（江苏省1994年竞赛题）　幂级数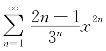的和函数为________.

解析　令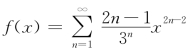，逐项求积分得

两边求导得

故原式＝.

例7.35（江苏省2006年竞赛题）　求幂级数的收敛域与和函数.

解析　令，则

设an＝n，因，故收敛半径R＝1.t＝1时（＊）式发散，故（＊）式的收敛域为［0，1）.由此可解得原级数的收敛域为，且

例7.36（北京市2001年竞赛题）　求的收敛区间与和函数.

解析　令，则

于是，原级数的收敛区间为（－∞，＋∞）.

因为

综上所述，和函数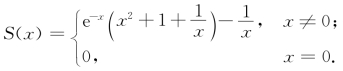

例7.37（南京大学1993年竞赛题）　幂级数的和函数为________，收敛域为________.(https://www.xing528.com)

解析　首先令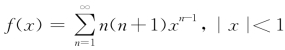.逐项求积分两次得

两边求导数两次得

于是原级数的和函数为，收敛域为（－1，1）.

例7.38（南京工业大学2009年竞赛题）　幂级数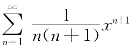在（－1，1）上的和函数为________________.

解析　令，逐项求导得

例7.39（江苏省1998年竞赛题）　求幂级数的收敛域与和函数.

解析　因为

又因为幂级数的收敛域为的收敛域为［－1，1），取它们的交集为（－1，1），于是和函数与收敛域为

例7.40（南京大学1995年竞赛题）　求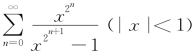的和函数.

解析　因为

所以原级数的部分和函数为

由于｜x｜＜1，所以，于是

例7.41（北京市1990年竞赛题）　对p讨论幂级数的收敛区间.

解析　令，则

所以幂级数的收敛半径R＝1.

当p＜0时，an→＼0（n→∞），所以幂级数在x＝±1处发散.因此，p＜0时，收敛区间为（－1，1）.

当0≤p＜1时，若x＝1，原幂级数为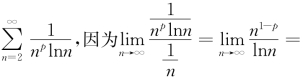发散；若是莱布尼兹型级数，故收敛.因此0≤p＜1时，收敛区间为［－1，1）.

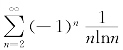当p＝1时，若x＝1，原级数化为，由积分判别法知发散；若x＝－1，为莱布尼兹型级数，故收敛.因此p＝1时，收敛区间为［－1，1）.

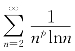当p＞1时，若收敛，由比较判别法可知收敛；若x＝－1，则绝对收敛.因此p＞1时，收敛区间为［－1，1］.

综上可知，p＜0时，收敛区间为（－1，1）；0≤p≤1时，收敛区间为［－1，1）；p＞1时，收敛区间为［－1，1］.

例7.42（北京市2004年竞赛题）　设

证明当｜x｜＜1时幂级数收敛，并求其和函数S（x）.

解析　因为，且

所以幂级数的收敛半径R＝1，故当｜x｜＜1时，幂级数收敛.

由，于是

考虑，逐项积分得

两边求导数得，所以

例7.43（浙江省2002年竞赛题）　设a1＝1，a2＝1，an＋2＝2an＋1＋3an，n≥1，求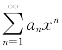的收敛半径、收敛域及和函数.

解析　由于an＋2＋an＋1＝3（an＋1＋an），令bn＝an＋1＋an，则

bn＋1＝3bn＝32bn－1＝…＝3nb1＝3n·2

考察

其中｜x｜＜1且｜3x｜＜1，故所求级数收敛半径为和函数为

例7.44（北京市1995年竞赛题）　已知a1＝1，a2＝1，an＋1＝an＋an－1（n＝2，3，…），试求级数的收敛半径与和函数.

解析　令.假设｛bn｝收敛，令bn→A（n→∞），则，由于bn＞0，故

下面来证明.由于1－A＝A2，0＜A＜1，故有

且的收敛半径

令原级数的和函数为S（x），由an＋1＝an＋an－1可知an＋2＝an＋1＋an，则an＝an＋2－an＋1，于是

综上所述，收敛半径，和函数为

例7.45（精选题）　设an是曲线y＝xn与y＝xn＋1（n＝1，2，…）所围区域的面积，记，求S1与S2的值.

解析　根据题意有

由于收敛，所以级数S1收敛；由于a2n－1＝收敛，所以级数S2收敛.有

由于级数显然是收敛的，所以加括号的级数也收敛，且

由于，收敛域为（－1，1］，所以，于是