例7.15(北方工业大学1999年竞赛题) 若级数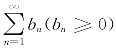 收敛,级数
收敛,级数![]() 也收敛,证明:级数
也收敛,证明:级数![]() 绝对收敛.
绝对收敛.
解析 由![]() 收敛,故其部分和数列
收敛,故其部分和数列
Sn=a1-a0+a2-a1+…+an-an-1=an-a0
收敛(当n→∞),于是存在A使![]() ,且存在M∈R+,使得|an|≤M.所以|anbn|≤M|bn|,根据比较判别法得
,且存在M∈R+,使得|an|≤M.所以|anbn|≤M|bn|,根据比较判别法得![]() 绝对收敛.
绝对收敛.
例7.16(广东省1991年竞赛题) 试判断级数![]() 是否收敛.若收敛,是绝对收敛还是条件收敛?
是否收敛.若收敛,是绝对收敛还是条件收敛?
解析 令![]() ,则
,则
显见an→0(n→∞),且数列{an}单调减(n=2,3,…).应用莱布尼兹判别法,得![]() 收敛.因为
收敛.因为
且![]() 发散,所以原级数非绝对收敛.故原级数条件收敛.
发散,所以原级数非绝对收敛.故原级数条件收敛.
例7.17(江苏省2006年竞赛题) 对常数p,讨论级数
何时绝对收敛、何时条件收敛、何时发散.
解析 令![]() ,则
,则
故当![]() 收敛,则原级数绝对收敛;当
收敛,则原级数绝对收敛;当![]()
![]() 发散,则原级数非绝对收敛.
发散,则原级数非绝对收敛.
当![]() 时显然an→0(n→∞).令
时显然an→0(n→∞).令
所以x充分大时f(x)单调增,于是n充分大时,![]() 单调减少,应用莱布尼兹判别法推知
单调减少,应用莱布尼兹判别法推知![]() 时原级数条件收敛.
时原级数条件收敛.
当![]() ,故
,故![]() 时原级数发散.
时原级数发散.
例7.18(全国大学生2013年决赛题) 若对于任意的趋向于0的序列{xn},级数![]() 都是收敛的,试证:级数
都是收敛的,试证:级数![]() 收敛.
收敛.
解析 (用反证法)设级数![]() 发散,记
发散,记![]() 于是存在单调增加的正整数数列{nk}(k=1,2,…),使得
于是存在单调增加的正整数数列{nk}(k=1,2,…),使得![]() (k=2,3,…).取
(k=2,3,…).取
则![]() .由于
.由于
所以级数![]() 发散,此与题设条件矛盾.所以级数
发散,此与题设条件矛盾.所以级数![]() 收敛.
收敛.
例7.19(江苏省1998年竞赛题) 设![]() 讨论级数
讨论级数![]() 是绝对收敛、条件收敛还是发散.
是绝对收敛、条件收敛还是发散.
解析 ![]() ,归纳设
,归纳设![]()
![]() 即an<an+1,数列{an}单调增加.又a1<2,归纳设an<2,则
即an<an+1,数列{an}单调增加.又a1<2,归纳设an<2,则![]() ,即an+1<2,所以数列{an}有上界.据单调有界准则得{an}收敛.令
,即an+1<2,所以数列{an}有上界.据单调有界准则得{an}收敛.令![]() ,则有
,则有![]() ,解得A=2.于是
,解得A=2.于是![]() .
.
令![]() ,由于
,由于
据比值判别法得![]() 收敛,即原级数绝对收敛.
收敛,即原级数绝对收敛.
例7.20(江苏省2012年竞赛题) 已知级数![]() 为条件收敛,求常数k的取值范围.
为条件收敛,求常数k的取值范围.
解析 令![]() ,因为
,因为
所以,当1-k>1,即k<0时,原级数绝对收敛;当1-k≤1,即k≥0时,原级数非绝对收敛.
当k≥1时,因为
所以,k≥1时原级数发散.
当0≤k<1时,因为![]() 为单调减少,应用莱布尼兹判别法得原级数收敛.
为单调减少,应用莱布尼兹判别法得原级数收敛.
综上,当0≤k<1时原级数条件收敛.
例7.21(江苏省1996年竞赛题) 设级数![]() 条件收敛,极限
条件收敛,极限![]() 存在,求r的值,并举出满足这些条件的例子.
存在,求r的值,并举出满足这些条件的例子.
解析 因级数![]() 条件收敛,故该级数不可能为正项级数或负项级数.由
条件收敛,故该级数不可能为正项级数或负项级数.由
(1)若|r|<1,则由比值判别法推得![]() 收敛,此与条件矛盾,故|r|≥1.
收敛,此与条件矛盾,故|r|≥1.
(2)若|r|>1,则由![]() ,推知n充分大时数列{|an|}单调增,故
,推知n充分大时数列{|an|}单调增,故![]() ,此与条件矛盾,故|r|=1,即r=1,-1.
,此与条件矛盾,故|r|=1,即r=1,-1.
(3)若r=1,则由![]() ,推知n充分大时,an与an+1同为正值或同为负值,此不可能.
,推知n充分大时,an与an+1同为正值或同为负值,此不可能.
综上,得r=-1.
例如级数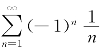 为条件收敛,且
为条件收敛,且
例7.22(江苏省1996年竞赛题) 讨论级数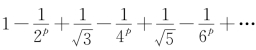 的敛散性(p为常数).
的敛散性(p为常数).
解析 当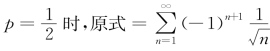 ,由于此为交错级数
,由于此为交错级数![]() 单调减少且收敛于0,由莱布尼兹判别法得
单调减少且收敛于0,由莱布尼兹判别法得![]() 时原级数收敛.
时原级数收敛.
当p≤0时,原级数的通项![]() ,所以原级数发散.
,所以原级数发散.
当![]() 时,考虑加括号(两项一括)的级数
时,考虑加括号(两项一括)的级数
由于n→∞时![]() 同阶,而
同阶,而![]() 同阶,
同阶,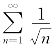 发散,所以
发散,所以![]() 时,加括号的级数(1)发散,因而原级数也发散.
时,加括号的级数(1)发散,因而原级数也发散.
当![]() 时,考虑如下加括号的级数
时,考虑如下加括号的级数
由于n→∞时![]() 同阶,而
同阶,而![]() 同阶,
同阶,![]() 发散,所以
发散,所以![]() 时,加括号的级数(2)发散,因而原级数也发散.
时,加括号的级数(2)发散,因而原级数也发散.
综上所述,原级数仅当![]() 时收敛.(https://www.xing528.com)
时收敛.(https://www.xing528.com)
例7.23(全国大学生2011年决赛题) 设函数f(x)是区间(-∞,+∞)上的可微函数,|f′(x)|<mf(x),其中0<m<1.任取实数a0,定义an=lnf(an-1),n=1,2,…,证明:![]() 绝对收敛.
绝对收敛.
解析 对函数F(x)=lnf(x),在以an-1,an-2为端点的区间上应用拉格朗日中值定理,得F(an-1)-F(an-2)=F′(ξ)(an-1-an-2),即
由于0<m<1时,几何级数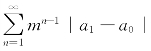 收敛,因此应用比较判别法可得级数
收敛,因此应用比较判别法可得级数![]() 收敛,即
收敛,即![]() 绝对收敛.
绝对收敛.
例7.24(精选题) 设f(x)在(-∞,+∞)上有定义,在x=0的邻域内f有连续的导数,且![]() ,讨论级数
,讨论级数![]() 的敛散性.
的敛散性.
解析 由于![]() ,所以x→0时
,所以x→0时![]() 而级数
而级数![]() 发散,故级数
发散,故级数![]() 非绝对收敛.由条件可得f(0)=0,又
非绝对收敛.由条件可得f(0)=0,又
且a>0,因f′(x)在x=0连续,所以存在x=0的某邻域U,其内f′(x)>0,因而在U中f(x)严格增,于是当n充分大时,有
即![]() 单调减,且
单调减,且![]() ,应用莱布尼兹法则即得原级数条件收敛.
,应用莱布尼兹法则即得原级数条件收敛.
例7.25(全国大学生2016年决赛题) 设![]() ,其中n为正整数.
,其中n为正整数.
(1)若n≥2,计算In+In-2;
(2)设p为实数,讨论级数![]() 的绝对收敛性与条件收敛性.
的绝对收敛性与条件收敛性.
解析 (1)应用定积分的换元积分法,可得
(2)当![]() 时,0≤tanx≤1,所以tann+2x≤tannx≤tann-2x,应用定积分的保向性得
时,0≤tanx≤1,所以tann+2x≤tannx≤tann-2x,应用定积分的保向性得
又由第(1)问可得![]() ,于是
,于是
①当p>1时,因为![]() ,而级数
,而级数
显然收敛,应用比较判别法得原级数绝对收敛.
②当0<p≤1时,因为![]() ,而级数
,而级数
显然发散,应用比较判别法得原级数非绝对收敛.由于
应用夹逼准则得![]() ,又数列
,又数列![]() 显然单调减少,据莱布尼茨判别法得原级数为条件收敛.
显然单调减少,据莱布尼茨判别法得原级数为条件收敛.
③当p≤0时,因为![]() ,所以
,所以![]() ≠0,因此原级数发散.
≠0,因此原级数发散.
例7.26(江苏省2002年竞赛题) 设k为常数,试判别级数![]() 的敛散性,何时绝对收敛?何时条件收敛?何时发散?
的敛散性,何时绝对收敛?何时条件收敛?何时发散?
解析 记![]() .当k>1时,因为
.当k>1时,因为
而级数![]() 收敛,所以k>1时
收敛,所以k>1时![]() 收敛,故原级数在k>1时绝对收敛.
收敛,故原级数在k>1时绝对收敛.
当k=1时,因为
故级数![]() 的部分和有上界,所以k=1时,
的部分和有上界,所以k=1时,![]() 收敛,故原级数在k=1时绝对收敛.
收敛,故原级数在k=1时绝对收敛.
当k<1时,因为
而![]() 发散,所以k<1时原级数非绝对收敛.
发散,所以k<1时原级数非绝对收敛.
当0≤k<1时,{an}单调减,且
应用莱布尼兹判别法得原级数在0≤k<1时条件收敛.
当k<0时,因为
所以k<0时原级数发散.
综上得:k≥1绝对收敛,0≤k<1时条件收敛,k<0时发散.
例7.27(江苏省2016年竞赛题) 已知级数![]() 其中实数λ∈[0,1],试对λ讨论该级数的绝对收敛、条件收敛与发散性.
其中实数λ∈[0,1],试对λ讨论该级数的绝对收敛、条件收敛与发散性.
解析 方法1 设![]() ,则an>0,且n→∞时
,则an>0,且n→∞时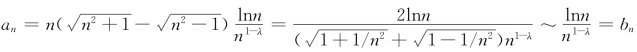 因为λ∈[0,1],即1-λ≤1,所以
因为λ∈[0,1],即1-λ≤1,所以![]() 发散,应用比较判别法得级数
发散,应用比较判别法得级数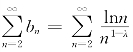 发散,再应用比较判别法得原级数非绝对收敛.
发散,再应用比较判别法得原级数非绝对收敛.
(1)当λ∈[0,1)时,令![]() ,当x≥2时,因
,当x≥2时,因
所以f(x)在x≥2时单调减少,故![]() 单调减少.
单调减少.
令![]() ,因0<1-λ≤1,则
,因0<1-λ≤1,则
所以x充分大时![]() 单调减少,故n充分大时
单调减少,故n充分大时![]() 单调减少.显然f(n)>0,g(n)>0,故{an}={f(n)·g(n)}也单调减少.又应用洛必达法则有
单调减少.显然f(n)>0,g(n)>0,故{an}={f(n)·g(n)}也单调减少.又应用洛必达法则有
应用莱布尼茨判别法得交错级数![]() 收敛.
收敛.
综上,可得原级数在λ∈[0,1)时为条件收敛.
(2)当λ=1时,因为
所以原级数在λ=1时发散.
方法2 数列{an}单调减少的证明改动如下,其他步骤同方法1.
所以x充分大时f(x)单调减少,故n充分大时{an}={f(n)}单调减少.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




