空间曲线方程、切线和例题解析

例6.25（南京大学1996年竞赛题）　记曲面z＝x2＋y2－2x－y在区域

D：x≥0，y≥0，2x＋y≤4

上的最低点P处的切平面为π，曲线在点（1，1，－2）处的切线为l，求点P到l在π上的投影l′的距离d.

解析　由解得驻点为.在驻点处

因Δ＝B2－AC＝－4＜0，且A＞0，所以为极小值，而驻点惟一，故为最小值，即点为曲面上最低点.

曲面在P点处的切平面π的方程为.

记P0为（1，1，－2），曲面x2＋y2＋z2＝6在P0的法向量n1与平面x＋y＋z＝0在P0的法向量n2分别为

故其交线在P0的切向量为

l＝n1×n2＝（2，2，－4）×（1，1，1）＝6（1，－1，0）

于是切线l的方程为

写为一般式为过直线l的平面束方程为

（x＋y－2）＋λ（z＋2）＝0

其法向量nλ＝（1，1，λ），令nλ⊥ηπ，ηπ＝（0，0，1），故λ＝0，即过l的平面x＋y－2＝0与平面π垂直，于是l在平面π内的投影l′的方程为

点到l′的距离为

例6.26（江苏省1998年竞赛题）　当k（＞0）取何值时，曲线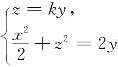是圆？并求此圆的圆心坐标以及该圆在zx平面、yz平面上的投影.

解析　题给曲线在xy平面上的投影为

它是xy平面上中心为，半轴长分别为的椭圆.设所求圆的圆心A的坐标为（a，b，c），由于点A在椭圆柱面的中心轴上，故a＝0，b＝欲使题给曲线为圆，等价于由此可解得k＝1.于是k＝1时，题给曲线为圆，圆心坐标为（0，1，1）.

将原方程组消去y，得圆在zx平面上的投影为

由于题给曲线圆在平面z＝y上，此平面垂直yz平面，所以圆在yz平面上的投影为一线段，即

例6.27（全国大学生2014年决赛题）　设F（x，y，z），G（x，y，z）有连续的偏导数过点P0（x0，y0，z0）.记Γ在xOy平面上的投影曲线为S，求S上过点（x0，y0）的切线方程.

解析　所求切线为Γ过点P0的切线在xOy平面上的投影，而Γ过点P0的切线为两个曲面的切平面的交线，即

两式消去z得

由于(www.xing528.com)

所以（＊）式即为所求切线的方程.

例6.28（江苏省2012年竞赛题）　已知点A（1，2，－1），B（5，－2，3）在平面Π：2x－y－2z＝3的两侧，过点A，B作球面Σ使其在平面Π上截得的圆Γ最小.

（1）求球面Σ的球心坐标与该球面的方程；

（2）证明：直线AB与平面Π的交点是圆Γ的圆心。

解析　（1），线段AB的中点是（3，0，1），于是线段AB的垂直平分面Π1的方程为x－y＋z＝4.

因球心在Π1上，设球心为O（a，b，4－a＋b），则OA2＝（a－1）2＋（b－2）2＋（5－a＋b）2.设球心O到平面Π的距离为d，则

设圆Γ的半径为r，则

化简得解得a＝8，b＝－2.因驻点是惟一的，圆Γ的半径r的最小值存在，故a＝8，b＝－2为所求的球心坐标分量，于是球心坐标为O（8，－2，－6）.因，所以球面方程为（x－8）2＋（y＋2）2＋（z＋6）2＝90.

（2）设直线AB的参数方程为x＝1＋t，y＝2－t，z＝－1＋t，代入平面Π的方程，解得t＝1，故直线AB与平面Π的交点M的坐标为M（2，1，0）.平面Π的法向量为n＝（2，－1，－2），因，显然OM⊥Π，于是点M是圆Γ的圆心.

例6.29（江苏省2006年竞赛题）　设圆柱面x2＋y2＝1（z≥0）被柱面z＝x2＋2x＋2截下的（有限）部分为Σ.为计算曲面Σ的面积，我们用薄铁片制作Σ的模型，A（1，0，5），B（－1，0，1），C（－1，0，0）为Σ上三点，将Σ沿线段BC剪开并展成平面图形D.建立平面直角坐标系，使D位于x轴的正上方，点A的坐标为（0，5）.试写出D的边界的方程，并求D的面积.

解析　圆柱面与柱面的交线Г在xy平面上的投影为圆（如下图（a）所示）Г1：x2＋y2＝1（z＝0），取M（1，0，0），在Г1上取点P（cost，sint，0），的弧长为t，过P 作PQ∥z轴，Q为PQ与Г的交点，Q的坐标为（cost，sint，（cost＋1）2＋1）.如下图（b）所示，在xy平面上展开后，P的坐标为（t，0），Q的坐标为（t，cos2t＋2cost＋2），故D的边界曲线由y＝cos2x＋2cosx＋2与x＝±π，y＝0组成.D的面积为

例6.30（江苏省2006年竞赛题）　设锥面z2＝3x2＋3y2（z≥0）被平面x－截下的（有限）部分为Σ.

（1）求曲面Σ的面积；

（2）用薄铁片制作Σ的模型为Σ上的两点，O为原点，将Σ沿线段OB剪开并展成平面图形D，以OA方向为极轴建立平面极坐标系，试写出D的边界的极坐标方程.

解析　（1）锥面与平面的交线在xy平面上的投影为此为一椭圆，它所围图形D1的面积为，Σ的面积为

（2）方法1　交线Г的球坐标方程为

作平面交Σ于Г1，Г1是半径为1的圆（如下图（a）所示），其上任一点到O的距离为2.在Г上取点P，设其球坐标为（r0，φ0，θ0），则.连接OP交Г1于Q，连接OA交Г1于A1，Q的球坐标为的弧长为θ0.

如上图（b），在平面图形D中，设P的极坐标为（ρ，θ），则Q的极坐标为（2，θ），的弧长为2θ，故θ0＝2θ.因r0＝ρ，于是D的边界的极坐标方程为

方法2　先求交线Г的柱坐标方程.令x＝ρ1cosθ，y＝ρ1sinθ，z＝z（这里（ρ1，θ，z）是Г上点的柱坐标），则Г的柱坐标方程为

作平面，交Σ于Г1，Г1为半径是1的圆（如图（a）所示），其上任一点到原点O的距离为2.在Г上任取点P，设其柱坐标为（ρ1，θ1，z1），连接OP交Г1于Q，连接OA交Г1交A1，则Q的柱坐标为的弧长为θ1.

如图（b），在平面图形D中，设P的极坐标为（ρ，θ），则Q的极坐标为（2，θ），的弧长为2θ，故θ1＝2θ.因为ρ2＝ρ21＋z2＝4ρ21，所以ρ＝2ρ1，于是D的边界曲线的极坐标方程为