空间曲面方程与切平面竞赛题解析

例6.13（江苏省2006年竞赛题）　已知空间三点A（－4，0，0），B（0，－2，0），C（0，0，2），O为原点，则四面体OABC的外接球面的方程为___________________.

解析　设四面体的外接球面的方程为

x2＋y2＋z2＋ax＋by＋cz＝0

将点A，B，C的坐标代入得到

16－4a＝0，　4－2b＝0，　4＋2c＝0

所以a＝4，b＝2，c＝－2，于是所求球面方程为

（x＋2）2＋（y＋1）2＋（z－1）2＝6

例6.14（南京大学1993年竞赛题）　曲面x2＋2y2＋3z2＝12的垂直于平面x＋4y＋3z＝0的法线方程为________________.

解析　平面的法向量为n＝（1，4，3），令F＝x2＋2y2＋3z2－12，则曲面的法向量为n1＝（F′x，F′y，F′z）＝（2x，4y，6z），令

得，代入曲面方程得t＝±2.由此得两个切平面的切点坐标为（1，2，1）与（－1，－2，－1）.于是两条法线方程为

例6.15（北京市1997年竞赛题）　证明曲面

上任意点处的切平面在Oz轴上的截距与切点到坐标原点的距离之比为常数，并求出此常数.

解析　记，则

曲面上任一点（x，y，z）处的切平面方程为

令X＝Y＝0，得该切平面在Oz轴上的截距为

于是截距与切点到原点的距离之比为.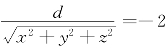

例6.16（南京大学1995年竞赛题）　从椭球面外的一点作椭球面的一切可能的切平面，证明全部切点在同一平面上.

解析　设椭球面Σ的方程为，椭球面外一点设为（如图所示）.由P向Σ作切平面，设切点为Q（x，y，z），因曲面Σ过点Q的切平面方程为

令（X，Y，Z）＝（x0，y0，z0），代入上式得

这表明切点Q位于同一平面（＊）上.

例6.17（江苏省2016年竞赛题）　设函数f（x，y）在点（2，－2）处可微，满足

f（sin（xy）＋2cosx，xy－2cosy）＝1＋x2＋y2＋o（x2＋y2）

这里o（x2＋y2）表示比x2＋y2高阶的无穷小（当（x，y）→（0，0）时），试求曲面z＝f（x，y）在点（2，－2，f（2，－2））处的切平面方程.

解析　因f（x，y）在点（2，－2）处可微，故f（x，y）在点（2，－2）处连续，又因

φ（x，y）＝sin（xy）＋2cosx，　ψ（x，y）＝xy－2cosy

在点（0，0）处连续，在原式中令（x，y）→（0，0）得f（2，－2）＝1.因f（x，y）在点（2，－2）处可微，所以f（x，y）在点（2，－2）处可偏导.因此，在原式中令y＝0得f（2cosx，－2）＝1＋x2＋o（x2），应用偏导数的定义得

在原式中令x＝0得f（2，－2cosy）＝1＋y2＋o（y2），应用偏导数的定义得

因此曲面z＝f（x，y）在点（2，－2，1）处的切平面方程为

化简得x－y＋z＝5.

例6.18（江苏省2002年竞赛题）　求直线绕y轴旋转一周所得旋转曲面的方程，并求该曲面与y＝0，y＝2所包围的立体的体积.

解析　如右图所示，在所求曲面上任取点P（x，y，z），过P点作垂直于y轴的平面，该平面与题给直线AB交于点M（x0，y0，z0），与y轴交于点Q（0，y，0），则y0＝y，且｜PQ｜＝｜MQ｜，所以.

因为

所以x0＝1＋2y，z0＝－y，由此可得旋转曲面方程为

x2＋z2＝1＋4y＋5y2

所求立体体积为

例6.19（江苏省2002年竞赛题）　设

（1）当k为何值时Г为一圆？

（2）当k＝6时，求Г的圆心和半径.

解析　（1）球面方程化为

（x＋2）2＋（y－2）2＋（z＋1）2＝9(www.xing528.com)

所以球面的球心为（－2，2，－1），半径为3.球心到平面2x＋y－2z＝k的距离为

由，解得k的取值范围是（－9，9）.

（2）k＝6时，上述d＝2，所以圆Г的半径.过球心与已知平面2x＋y－2z＝6垂直的直线为

x＝－2＋2t，　y＝2＋t，　z＝－1－2t

代入平面方程解得，故所求圆的圆心为，半径.

例6.20（全国大学生2015年预赛题）　设M是以三个正半轴为母线的半圆锥面，求其方程.

解析　圆锥面M的顶点为O（0，0，0），其准线选作过三点（1，0，0），（0，1，0），（0，0，1）的圆

设P（x，y，z）是圆锥面M上的任一点，射线OP与准线Γ的交点记为Q（x1，y1，z1），则

由于消去t即得所求圆锥面M的方程为xy＋yz＋zx＝0

例6.21（北京市1999年竞赛题）　表面为旋转曲面的镜子应具有怎样的形状才能使它将所有平行于其轴的光线反射到一点？求出旋转曲面的方程.

解析　如图，设旋转曲面的旋转轴为x轴，旋转曲面与xy平面的截线为Γ，设Γ的方程为y＝y（x），入射光线L1平行于x轴，反射光线L2经过定点O（0，0）.

Γ在点P（x，y（x））的切线为L，则L的方向向量为l＝（－1，－y′（x）），L1的方向向量为l1＝（－1，0），L2的方向向量为l2＝（－x，－y（x））.L与L1的夹角

L与L2的夹角

由于θ1＝θ2，所以

化简得y（x）满足微分方程

令y＝xu，方程化为

令1＋u2＝v2（v＞0），方程化为

解得（v－1）x＝C，即y2＝2Cx＋C2，于是旋转曲面的方程为

y2＋z2＝2Cx＋C2

例6.22（北京市2001年竞赛题）　若可微函数f（x，y）对任意的x，y，t满足f（tx，ty）＝t2f（x，y），P0（1，－2，2）是曲面z＝f（x，y）上的一点，且＝4，求曲面在P0处的切平面方程.

解析　由f（tx，ty）＝t2f（x，y），两边对t求偏导有

取t＝1，x＝1，y＝－2，得

将代入上式，得，故曲面在P0处的法向量为，于是所求切平面的方程为

4（x－1）－（z－2）＝0，　即　4x－z－2＝0

例6.23（江苏省2008年竞赛题）　（1）证明曲面Σ：

x＝（b＋acosθ）cosφ，　y＝asinθ，　z＝（b＋acosθ）sinφ

（0≤θ≤2π，0≤φ≤2π；0＜a＜b）

为旋转曲面；

（2）求旋转曲面Σ所围立体的体积.

解析　（1）消去θ，φ，得

它是曲线绕y轴旋转一周生成的旋转曲面.

（2）

例6.24（浙江省2007年竞赛题）　有一张边长为4π的正方形纸（如下图所示），C，D分别为AA′，BB′的中点，E为DB′的中点.现将纸卷成圆柱形，使A与A′重合，B与B′重合，并将圆柱面垂直放在xOy平面上，且B与圆点O重合，D落在y轴正向上，此时求：

（1）通过C，E两点的直线绕z轴所得的旋转曲面方程；

（2）此旋转曲面与xOy平面和过A点垂直于z轴的平面所围成的立体体积.

解析　（1）依题意可知圆柱底面的半径R＝2，故C点坐标取为（0，4，4π），E点坐标为（2，2，0）＝（－2，2，4π），因此过C，E两点的直线方程为

所以旋转曲面方程为

（2）如右上图，旋转曲面在垂直于z轴方向的截面是一个半径为的圆，故所求体积V为