重积分不等式证明详解-高数竞赛题解-2018

例5.29（北京市2001年竞赛题）　设f（x）是［0，1］上的连续函数，证明：

解析　原式可化为下面两种形式的二重积分：

其中D为0≤x≤1，0≤y≤1，于是

例5.30（清华大学1985年竞赛题）　设函数f（x）在［0，1］上连续且单调减，又f（x）＞0，求证：并给予物理解释.

解析　由于f（x）＞0，f（y）＞0，［f（x）－f（y）］（x－y）≤0，所以

应用二重积分的保向性，取D：｛（x，y）｜0≤x≤1，0≤y≤1｝，则

物理解释：两根长为1的直杆放在x轴的区间［0，1］上，第一根直杆的线密度函数为f2（x），其重心坐标为x1，第二根直杆的线密度函数为f（x），其重心坐标为x2，则x1≤x2，这里

例5.31（莫斯科化工机械学院1977年竞赛题）　求证不等式

解析　取D＝｛（u，v）｜0≤u≤x，0≤v≤x｝，则

取D1＝｛（u，v）｜u2＋v2≤x2，u≥0，v≥0｝，D2＝｛（u，v）｜u2＋v2≤2x2，u≥0，v≥0｝，则D1为D的真子集，D为D2的真子集，而，所以

综合（1），（2），（3）式即得原不等式成立.

例5.32（广东省1991年竞赛题）　设D域是x2＋y2≤1，试证明不等式

解析　运用极坐标变换，有

下面先证明：x≥0时，有令f（x）＝x－sinx，则f′（x）＝1－cosx≥0，于是f（x）单调增加，f（x）≥f（0）＝0，即sinx≤x.令g（x），于是g′（x）单调增加，g′（x）≥g′（0）＝0，g（x）单调增加，g（x）≥g（0）＝0，即取

设原二重积分的值为I，于是

即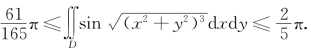

例5.33（江苏省2004年竞赛题）　求证，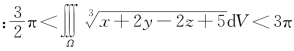

其中Ω为x2＋y2＋z2≤1.(www.xing528.com)

解析　首先求f＝x＋2y－2z＋5在x2＋y2＋z2≤1上的最大值与最小值.在x2＋y2＋z2＜1的内部，由于

故f在x2＋y2＋z2＜1上无驻点.在x2＋y2＋z2＝1上应用拉格朗日乘数法，令

F＝x＋2y－2z＋5＋λ（x2＋y2＋z2－1）

由

解得可疑的条件极值点由于连续函数f在有界闭集x2＋y2＋z2＝1上有最大值和最小值，所以f（P1）＝8，f（P2）＝2分别是f的最大值与最小值.又由于f与有相同的极值点，故

由积分的保向性得

例5.34（全国大学生2014年决赛题）　设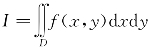，其中

函数f（x，y）在D上有连续的二阶偏导数.若对任何x，y有f（0，y）＝f（x，0）＝0，且

解析　将二重积分化为二次积分，再分部积分得

例5.35（广东省1991年竞赛题）　设二元函数f（x，y）在区域D＝｛0≤x≤1，0≤y≤1｝上具有连续的四阶偏导数，并且f（x，y）在区域D的边界上恒为0，且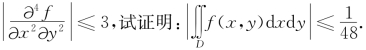

（提示：考虑二重积分

解析　考察上述二重积分，运用分部积分法，有

例5.36（全国大学生2015年预赛题）　设f（x，y）在x2＋y2≤1上有连续的二阶偏导数M，证明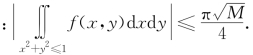

解析　将函数f（x，y）在（0，0）处展为一阶马克劳林展开式，有

应用柯西－施瓦兹不等式得

所以