高等数学竞赛题解析教程.2018：二重积分的计算题

例5.1（浙江省2011年竞赛题）　计算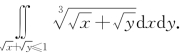

解析　化为先对y后对x的二次积分计算，有

例5.2（江苏省2017年竞赛题）　设函数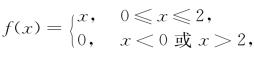试求二重积分

解析　根据题意可得

设D′＝｛（x，y）｜0≤x＋y≤2，x2＋y2≤4｝，则原式用坐标轴将区域D′分为D1，D2，D3（如图）.用极坐标计算得

例5.3（南京工业大学2009年竞赛题）　求

解析　记D为x＋y＝t（t＞0）与x轴、y轴所围的区域，则

由于在区域D上连续，应用二重积分中值定理，有

这里（ξ，η）∈D，于是

例5.4（天津市2003年竞赛题）　计算

其中，且a，b，φ均为常数.

解析　原式中两项分别表示函数在图中D1与D2区域上的两次积分，D＝D1＋D2，化为极坐标计算，有

注：原题中将积分下限ycotφ错写为ytanφ.

例5.5（江苏省2012年竞赛题）　计算二重积分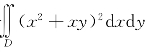，其中D为｛（x，y）｜x2＋y2≤2x｝.

解析　曲线x2＋y2＝2x的极坐标方程为ρ＝2cosθ，区域D关于y＝0对称，2x3y关于y＝0为奇函数，x2（x2＋y2）关于y＝0为偶函数，应用奇偶对称性，得

其中.由于

因此.又因为，所以

故原式＝.

例5.6（江苏省2002年竞赛题）　求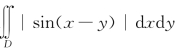，其中D：x≥0，.

解析　如图，用直线y＝x将区域D分割为D1与D2，则在D1上，在D2上，于是

例5.7（江苏省2006年竞赛题）　设D为y＝x，x＝，y＝0所围的平面图形，求(https://www.xing528.com)

解析　用将D分为D1＋D2（如图所示），则

例5.8（江苏省2016年竞赛题）　设D＝｛（x，y）｜0≤y≤1－x，－1≤x≤1｝，试求二重积分

解析　在D内作圆x2＋y2＝1使其分为D1与D2（如右图所示），于是

例5.9（江苏省2016年竞赛题）　设D＝｛（x，y）｜0≤y≤1－x，0≤x≤1｝，试求二重积分

解析　在D内作圆x2＋y2＝x使其分为D1与D2（如右图所示），圆x2＋y2＝x与直线y＝1－x的交点分别为于是

再用线段OA将D1分为σ1与σ2（如图），则

例5.10（全国大学生2013年决赛题）　求二重积分

解析　在圆D：x2＋y2≤1内作圆x2＋y2－x－y＝0，即

使其分为D1与D2（如上图所示），由于圆D1在原点处的切线是第Ⅱ，Ⅳ象限的角平方线，于是

例5.11（全国大学生2009年初赛题）　计算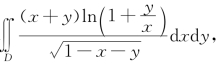其中区域D为直线x＋y＝1与两坐标轴所围的三角形区域.

解析　运用极坐标计算，记φ（θ）＝cosθ＋sinθ，则

例5.12（莫斯科技术物理学院1977年竞赛题）　设Г为圆x2＋y2＝4，现引入函数ρ（x，y），其绝对值等于点（x，y）到曲线Г的距离，其符号按下列方法确定：当点（x，y）在圆Г的内部时取负号，当点（x，y）在圆Г的外部时取正号.已知常数a：0＜a＜2，求二重积分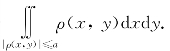

解析　设（ρ，θ）为点（x，y）的极坐标，且

则当（x，y）∈D时，ρ（x，y）＝ρ－2，于是

例5.13（江苏省2002年竞赛题）　设f（u）在u＝0可导，f（0）＝0，D：x2＋

解析　首先采用极坐标计算二重积分，有

例5.14（浙江省2010年竞赛题）　计算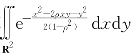，其中0≤ρ＜1.

解析　运用二重积分换元积分法，令x＝t＋s，y＝t－s，则雅可比行列式J＝－2，面积微元为dxdy＝｜J｜dtds＝2dtds，于是

再运用换元积分法，令，则面积微元为dtds＝并采用极坐标计算，有