【摘要】：，9）中取得，于是有例4.42用拉格朗日乘数法求函数f（x，y）＝x2＋在区域x2＋2y2≤4上的最大值与最小值.解析在x2＋2y2＜4内，由得惟一驻点P1（0，0）.在x2＋2y2＝4上，令将4（1＋λ）乘以式减去乘以式，得x＝0.若8λ2＋16λ＋6≠0，则x＝0，由和式得y＝0，与式矛盾.故8λ2＋16λ＋6＝0，解得.当时解得驻点当时解得驻点又f＝0，f＝2，f＝2，f＝6，f＝6，故fmin＝0，fmax＝6
例4.41（莫斯科自动化学院1975年竞赛题） 求函数z＝x2＋y2－xy在区域D：｜x｜＋｜y｜≤1上的最大值与最小值.
解析 首先在D的内部：｜x｜＋｜y｜＜1，由
解得驻点P1（0，0）.
在边界x＋y＝1（0＜x＜1）上，令
F＝x2＋y2－xy＋λ（x＋y－1）
由
解得拉格朗日函数F的驻点
同上，在边界y－x＝1（－1＜x＜0）上，可求得相应的拉格朗日函数的驻点
；在边界－x－y＝1（－1＜x＜0）上，可求得相应的拉格朗日函数的驻点
；在边界x－y＝1（0＜x＜1）上，可求得相应的拉格朗日函数的驻点
.又记四个边界线段的交点分别为P6（1，0），P7（0，1），P8（－1，0），P9（0，－1）.
函数z（x，y）的最大值与最小值只能在上述9个点Pi（i＝1，2，…，9）中取得，于是有(www.xing528.com)
例4.42（江苏省2006年竞赛题） 用拉格朗日乘数法求函数f（x，y）＝x2＋
在区域x2＋2y2≤4上的最大值与最小值.
解析 在x2＋2y2＜4内，由
得惟一驻点P1（0，0）.在x2＋2y2＝4上，令
将4（1＋λ）乘以（1）式减去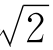
乘以（2）式，得（8λ2＋16λ＋6）x＝0.若8λ2＋16λ＋6≠0，则x＝0，由（1）和（2）式得y＝0，与（3）式矛盾.故8λ2＋16λ＋6＝0，解得
.
当
时解得驻点
当
时解得驻点
又f（P1）＝0，f（P2）＝2，f（P3）＝2，f（P4）＝6，f（P5）＝6，故
fmin＝0， fmax＝6
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
