高数竞赛题解析：求二元函数极值

例4.33（江苏省2017年竞赛题）　求函数f（x，y）＝3（x－2y）2＋x3－8y3的极值，并证明f（0，0）＝0不是f（x，y）的极值.

解析　由解得驻点P1（－4，2），P2（0，0）.因为

在P1处，A＝－18，B＝－12，C＝－72，Δ＝B2－AC＝－1152＜0，且A＜0，所以f（－4，2）＝64为极大值；在P2处，A＝6，B＝－12，C＝24，Δ＝B2－AC＝0，所以使用Δ不能证明f（0，0）不是极值.

下面用极值的定义来判断.任取（0，0）的去心邻域

（1）在y＝0上，取，则当n充分大时，显然有，且

（2）在x＝ky（0＜k＜2）上，有，故取，即取

时有

又因为

所以当k小于2且充分接近2时

由上述（1）和（2）可得，在P2（0，0）的任意小邻域内，既存在点（xn，yn），使得f（xn，yn）＞0，也存在点（xk，yk），使得f（xk，yk）＜0，故f（0，0）＝0不是极值.

例4.34（江苏省2006年竞赛题）　函数f（x，y）＝e－x（ax＋b－y2）中常数a，b满足条件______________时，f（－1，0）为其极大值.

解析　应用二元函数取极值的必要条件得

所以b＝2a.由于

令Δ＜0，A＜0，解得a＞0，b＝2a为所求条件.当a＜0时推得Δ＞0，此时函数f在（－1，0）不取极值；当a＝0，b＝0时推得Δ＝0，此时f（x，y）＝－y2e－x≤f（－1，0）＝0，故f（－1，0）也是极大值.于是a≥0，b＝2a为所求.

例4.35（南京大学1993年竞赛题）　求曲线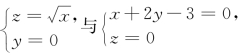的距离.

解析　设A（p，q，r）与B（u，v，w）分别为两曲线上的任意点，F为A，B两点距离的平方，于是

F＝（p－u）2＋（q－v）2＋（r－w）2

由条件知，q＝0，u＝3－2v，w＝0，代入上式得

F＝（p－3＋2v）2＋v2＋p

由

可解得惟一驻点.从几何意义知F的最小值存在，故在两曲线上对应的点与（1，1，0）之间的距离最小，其值为，即两曲线的距离为.(www.xing528.com)

例4.36（北京市1993年竞赛题）　求使函数

达到最大值的（x0，y0）以及相应的f（x0，y0）.

解析　方法1　记g（x，y）＝lnf（x，y），则

且g（x，y）与f（x，y）有相同的极大值点.由于

令，解得驻点

当y＞0时，因为

因，故f（x，y）在点达到极大值，有在半平面y＞0上，f（x，y）可微，且驻点惟一，故是f（x，y）在y＞0上的最大值.

当y＜0时，因为

因，同理可得是f（x，y）在y＜0上的最大值.

综上，由于因此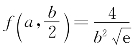是函数f（x，y）的最大值.

方法2　驻点的求法同方法1.

当y≠0时，f（x，y）可微.∀c∈R，当（x，y）→（c，0）时，由于

其中，且y→0时，t→∞.令，应用洛必达法则，有

所以，于是

例4.37（江苏省2010年竞赛题）　如图，ABCD是等腰梯形，BC∥AD，AB＋BC＋CD＝8，求AB，BC，AD的长，使该梯形绕AD旋转一周所得旋转体的体积最大.

解析　令BC＝x，AD＝y（0＜x＜y＜8）^[2]，则.设BE⊥AD，则

由

解得惟一驻点P（2，4），由于

又，A＜0，所以x＝2，y＝4时V取最大值.于是AB＝3，BC＝2，AD＝4为所求的值.