高等数学竞赛题解析：积分等式证明

例3.103（精选题）　设f（x）在［a，b］上具有连续的2阶导数，且f′（a）＝f′（b）＝0，求证：∃ξ∈（a，b），使得

解析　令则F′（x）＝f（x），F″（x）＝f′（x），F‴（x）＝f″（x），且F（a）＝0，F″（a）＝F″（b）＝0.函数F（x）在x＝a处的2阶泰勒展式为

这里ξ1介于a与x之间.令x＝b得

这里a＜ξ2＜b.函数F（x）在x＝b处的2阶泰勒展式为

这里η1介于x与b之间.令x＝a得

这里a＜η2＜b.（1）式减（2）式，得

若f″（ξ2）＝f″（η2），则ξ＝ξ2或ξ＝η2，代入（3）式即得原式；若f″（ξ2）≠f″（η2），由于f″（x）在［a，b］上连续，由最值定理，f″（x）在［a，b］上有最大值M与最小值m，则

再应用介值定理，∃ξ∈（a，b），使得

于是有

例3.104（精选题）　设函数f（x）在闭区间［a，b］上具有连续的2阶导数，求证：∃ξ∈（a，b），使得

解析　令，则F′（x）＝f（x），F″（x）＝f′（x），F‴（x）＝f″（x），且F（a）＝0.F（x）在处的2阶泰勒展式为

这里ξ1介于x与之间.在（1）式中令x＝a，得

这里在（1）式中令x＝b，得(www.xing528.com)

这里（3）式减去（2）式，得

由于f″（x）在［a，b］上连续，由最值定理，f″（x）在［ξ2，ξ3］上有最大值M与最小值m，则

再应用介值定理，∃ξ∈（ξ2，ξ3）⊂（a，b），使得

于是有

例3.105（全国大学生2012年决赛题）

（1）求解微分方程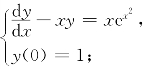

（2）如果y＝f（x）为上述方程的解，证明

解析　（1）这是一阶线性非齐次方程，易于求得解为y＝ex2（过程从略）.

（2）对函数f（x）＝ex2在区间［0，x］（0≤x≤1）上应用拉格朗日中值定理，必∃ξ∈（0，x），使得f（x）－f（0）＝f′（ξ）x，即

应用定积分的保号性，有

由于

再应用夹逼准则，得