高等数学竞赛题解析教程2018：积分不等式的证明全解

例3.77（江苏省1994年竞赛题）　试证明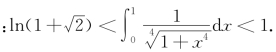

解析　当，所以

例3.78（浙江省2011年竞赛题）　设f：［0，1］→［－a，b］连续，且＝ab，证明：

解析　由－a≤f（x）≤b，可得，于是

展开得

例3.79（全国大学生2014年决赛题）　设f（x）是闭区间［0，1］上的连续函数，且满足，求函数f（x），使得取得最小值.

解析　应用柯西－施瓦兹不等式，有

由此可得的最小值为.因此，只要函数f（x）满足

故所求函数为

例3.80（江苏省2017年竞赛题）　已知函数f（x）在区间［a，b］上连续并单调增加，求证：

解析　方法1　原式等价于

令

应用变限定积分的导数公式得

对于上式中的定积分应用积分中值定理，则存在ξ∈（x，b），使得

于是

F′（x）＝－n（b－x）nf（ξ）＋n（b－x）nf（x）＝n（b－x）n［f（x）－f（ξ）］≤0

因此F（x）在［a，b］上单调减少，由此可得

此式等价于原式成立.

方法2　作积分变换，令，则x＝b－（b－a）t，并应用函数f（x）的单调增加性，有

令b－（b－a）tn＋1＝u，上式右端化简得

方法3　已知f（x）单调增加，设g（x）单调减少，则∀x，y∈［a，b］，有

记D＝｛（x，y）｜a≤x≤b，a≤y≤b｝，应用二重积分的保向性得

上式中

于是有不等式

两端消去因子b－a即得原不等式成立.

例3.81（莫斯科全苏大学生1976年竞赛题）　已知函数f（x）定义于［0，1］且单调减、可积，求证：

解析　（这里没有f连续的条件，所以不能使用积分中值定理）由于f（x）单调减，故有

于是有

例3.82（南京大学1996年竞赛题）　设函数y＝f（x）在［0，＋∞）上连续，且严格增，f（0）＝0，f－1是f的反函数，证明：对任意a＞0，b＞0，恒有

解析　（1）若f（a）≤b，首先从几何上由右图可看出

下面给出证明：

在（1）式右端第一个积分中，令x＝f－1（y），则

在（1）式右端的第二个积分中，因f－1（y）严格增，故f－1（y）≥f－1（f（a））＝a，得

将（2），（3）两式代入（1）式得

移项即得

（2）若f（a）＞b，从几何上由右图可看出

下面给出证明：

因f（a）＞b，所以a＞f－1（b），则

在（4）式右端的第一个积分中，令y＝f（x），则

在（4）右端的第二个积分中，因f（x）≥b，所以

将（5），（6）两式代入（4）式得

例3.83（莫斯科电气学院1976年竞赛题）　证明

解析　令x2＝t，则

对于上式右端的第二项，令t－π＝u，则

所以（＊）式右端是常义定积分，且在（0，π）上连续，故

例3.84（莫斯科钢铁与合金学院1977年竞赛题）　求证：

解析　令x＝sint，则

令x＝cost，则

令，则由，又f″（t）＝sint＋cost＞0，则为极小值，故所以

例3.85（精选题）　已知函数f（x）在上连续（a＞0），且f（x）≥0，求证

解析　当时

又f（x）≥0，所以，即

应用定积分的保向性，上式两边从到a积分得

例3.86（全国大学生2015年预赛题）　设f（x）在［0，1］上连续.求证：（1）∃ξ∈［0，1］，使得｜f（ξ）｜＞4；（2）∃η∈［0，1］，使得｜f（η）｜＝4.

解析　（1）（反证法）设∀x∈［0，1］，有｜f（x）｜≤4.由于

所以

于是.而此与条件矛盾，故∃ξ∈［0，1］，使得｜f（ξ）｜＞4.

（2）因f∈C［0，1］，故｜f（x）｜∈C［0，1］.应用积分中值定理，∃λ∈（0，1），使得

于是｜f（λ）｜＝0.对连续函数｜f（x）｜，因｜f（λ）｜＝0，｜f（ξ）｜＞4，应用介值定理，∃η∈［0，1］，使得｜f（η）｜＝4.

例3.87（南京大学1993年竞赛题）　证明：

解析　令，并应用奇函数在对称区间上积分的性质，有

代入原式左边，应用柯西－施瓦兹不等式得

例3.88（精选题）　设函数f（x）在［a，b］上可导，f′（x）在［a，b］上可积，且f（a）＝f（b）＝0，求证：∀x∈［a，b］，有

解析　由于

所以∀x∈［a，b］，有

两式相加得

即

例3.89（莫斯科铁路运输工程学院1975年竞赛题）　设函数f（x）在［0，2］上连续可导，f（0）＝f（2）＝1，｜f′（x）｜≤1，求证.

解析　当0≤x≤1时，应用拉格朗日中值定理，有(www.xing528.com)

f（x）＝f（0）＋f′（ξ）x＝1＋f′（ξ）x　（0＜ξ＜x）

则1－x≤f（x）≤1＋x.当1≤x≤2时，应用拉格朗日中值定理，有

f（x）＝f（2）＋f′（η）（x－2）＝1＋f′（η）（x－2）　（x＜η＜2）

则x－1≤f（x）≤3－x.于是

上式中取不等号“＜”，是因为不可能出现

的情况（此时f（x）在x＝1处不可导）.同样，有

上式中取不等号“＞”，是因为不可能出现

的情况（此时f（x）在x＝1处不可导）.

例3.90（浙江省2005年竞赛题）　证明：对任意连续函数f（x），有

于是

例3.91（莫斯科大学1977年竞赛题）　设函数f（x）在［0，1］上连续可导，求证：

解析　（1）若f（x）在（0，1）上满足f（x）＞0或f（x）＜0，则

（2）若上述（1）不成立，应用零点定理知∃c∈（0，1），使得f（c）＝0，且

这里x∈［0，1］.于是

上式两边从0到1积分得

由（1）与（2）即得

例3.92（江苏省2008年竞赛题）　设f（x）在［a，b］上具有连续的导数，求证：

解析　方法1　应用积分中值定理，∃ξ∈（a，b），使得

方法2　由f（x）在［a，b］上连续，可得｜f（x）｜在［a，b］上连续，根据最值定理，∃x0∈［a，b］，使得.因为

例3.93（南京大学1996年竞赛题）　设f（a）＝0，f（x）在［a，b］上的导数连续，求证：

解析　应用拉格朗日中值定理，∃ξ∈（a，x），这里a＜x≤b，使得

f（x）－f（a）＝f′（ξ）（x－a）⇒｜f（x）｜≤M｜x－a｜

这里（由于｜f′（x）｜在［a，b］上连续，所以｜f′（x）｜在［a，b］上有最大值M）.上式两边从a到b积分得

例3.94（莫斯科大学1977年竞赛题）　设函数f（x）在区间［a，b］上连续可导，且f（a）＝f（b）＝0，求证：

解析　因｜f′（x）｜在［a，b］上连续，应用最值定理，有

存在.∀x∈（a，b），则有

f（x）＝f（a）＋f′（ξ）（x－a）＝f′（ξ）（x－a）

f（x）＝f（b）＋f′（η）（x－b）＝f′（η）（x－b）

这里a＜ξ＜x，x＜η＜b.于是有

｜f（x）｜≤M（x－a），　｜f（x）｜≤M（b－x）

∀x0∈（a，b），则

令，则u′＝2x0－（a＋b）.由u′＝0得驻点x0＝，又u″＝2＞0，所以为u的最小值.

由于（＊）式对（a，b）中的任意x0皆成立，取，即得

例3.95（北京市1990年竞赛题）　设函数f（x）在区间［a，b］上连续，且对于t∈［0，1］及x1，x2∈［a，b］满足

f（tx1＋（1－t）x2）≤tf（x1）＋（1－t）f（x2）

证明：

解析　令x＝a＋t（b－a），则有

所以

右边不等式得证.又令x＝a＋b－u，有

左边不等式得证.

例3.96（北京市1990年竞赛题）　设f（x）是定义在区间［0，1］上的连续函数，且0＜m≤f（x）≤M，对于x∈［0，1］，证明：

例3.97（北京市1996年竞赛题、全国大学生2016年预赛题）　设f（x）是区间［0，1］上的连续可微函数，且当x∈（0，1）时，0＜f′（x）＜1，f（0）＝0，证明：

解析　利用柯西－施瓦兹不等式有

从而左边不等式成立.构造

因为0＜f′（x）＜1，f（0）＝0⇒f（x）严格增⇒f（x）＞f（0）＝0，于是G′（x）＞0⇒G（x）严格增⇒G（x）＞G（0）＝0⇒F′（x）＞0，从而F（x）严格增⇒F（1）＞F（0）＝0，即

从而右边不等式得证.

例3.98（精选题）　设f（x）二阶可导，f″（x）≥0，g（x）为连续函数，a＞0，求证：

解析　f（x）在x＝x0处的一阶泰勒展式为

这里ξ介于x与x0之间.令则

应用定积分的保向性，此式两边从0到a积分得

例3.99（精选题）　设函数f（x）在［a，＋∞）上二阶可导，M1＞0，M2＞0，且｜f（x）｜≤M1，｜f″（x）｜≤M2，求证：∀x∈［a，＋∞），有

解析　∀x0∈［a，＋∞），f（x）在x＝x0处的一阶泰勒展式为

这里ξ介于x与x0之间，所以

的惟一解为所以g（h）的最小值为g（h0）于是

由x0∈［a，＋∞）的任意性即得∀x∈［a，＋∞），有

例3.100（精选题）　设f（x）在［0，1］上2阶连续可导，f（0）＝0，f（1）＝0，且∀x∈（0，1）有f（x）≠0，求证

解析　由于f（x）在（0，1）上连续，且f（x）≠0，所以f（x）在（0，1）上不变号，不妨设∀x∈（0，1）有f（x）＞0.应用最值定理，f（x）在［0，1］上有最大值，设

在［0，x0］与［x0，1］上分别应用拉格朗日中值定理，则∃α∈（0，x0）和β∈（x0，1），使得

代入（＊）式即得

例3.101（北京市1993年竞赛题）　求证

解析　运用eu的马克劳林级数，有

由于n＝2k＋1（k＝0，1，2，…）时，有

当n＝2k（k＝1，2，…）时，有

因此，由逐项积分有

得证.

例3.102（浙江省2006年竞赛题）　求最小的实数C，使得满足的连续函数f（x），都有

解析　因为